The physics of the goal
The past Football Worldcup has aroused many passions. Let's see if this post can awake some passion for physics.
 [1]
[1]
When our favorite team scores, we hardly think about the physical laws that can explain the trajectory that the ball described to finish inside the goal. We simply jump out of our seat and celebrate. Although there are many times we marvel at the curve that describes a ball on its flight. In some cases it happens that the intuitive calculation fails, then the goalkeepers can be surprised by shots that seemed easy to control, but eventually slip into the goal.
But let's go in parts. To introduce ourselves to the physics behind the goal, we will evaluate different types of executions, starting from the simplest (in physical terms) to the most complex.
Penalty Kick (Uniform Rectilinear Motion)
The first case we will analyze is the penalty. This is a shot that runs at a distance of approximately 11 meters from the goal. To evaluate most of this kind of shots we will get to identify the trajectory of the ball as a straight line. In addition, considering the short distance and the force with which the ball is usually kicked, we will assume that the speed of the ball when leaving the foot is the same as that of arrival at the goal. So it’s a case of uniform rectilinear motion.
Thus, the physical laws that come into question in these shots are very simple and to evaluate them it’s enough to use the following equation: X = Xi + V.t (1)
Where:
- X and Xi represent the position of the ball at a given moment (X) and at the initial moment (Xi)
- V represents the velocity, which in this case is a constant (does not vary in the whole journey).
- t is the time elapsed from the initial moment.
So, for example, if the ball is driven with a velocity (V) of about 100 km /h (about 28 m/s) we can use the previous equation to calculate how long it will take the ball to reach the goal.
Clearing t from equation (1): t = (X - Xi) / V, then t = 11 m / (28m / s) = 0.39 s
Now, the exact distance that the ball will travel until it reaches the goal will depend on the angle with which it is kicked; It will only be 11 meters if it is kicked straight to the goal and without rising from the floor. But starting from the distance between the penalty point and the goal at its midpoint (11 meters) and the dimensions of the goal (7.32 long x 2.44 high), we can determine the length of any other alternative trajectory of the ball. For this we will see that we simply have to use the famous Pythagorean Theorem: the sum of the squares of the legs is equal to the square of the hypotenuse.
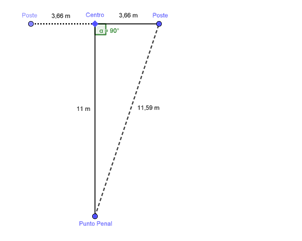
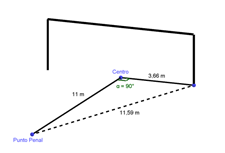
Looking at the graph, we can see that the alternative paths trace a right triangle, where the legs are the distance from the penalty point to the goal and the distance from the center of the goal to the point by which the ball crosses the line of the goal. If the ball enters at the height of the floor and next to one of the posts, it would be: √ [(11 m) ² + (3.66 m) ²] = √134.3956 = 11.59 m
A similar calculation will allow us to evaluate the distance if the ball crosses the goal at a certain height between the floor and the crossbar. Suppose you hit the top angle of the goal, then we will take the calculated 11.59 m just as one of the legs and the height of the goal (2.44 m) will be the other leg. So, the distance if the ball goes any of the two superior angles will be: √ (11,59 m) ² + 2,44 m) ² = 11,84 m
Chip Shot (Parabola)
The next case that we will evaluate is the the goal that is made with a chip shot. This shot is characterized by the subtlety of its execution. It can take place when the goalkeeper is at a certain distance from the goal (perhaps imprudently) and the kicker. and sometimes can be surprised by a shot of this type, in which the executor hit the ball in a way that describes a parabola that exceeds the height of the goalkeeper and then reaches the goal below the crossbar.
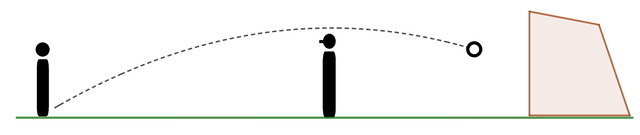
It is a clear example of what in physics is called parabolic motion. In these cases in addition to the strength of the foot that drives the ball, we must consider the intervention of another force: gravity.[2] To simplify the calculations we will not consider here the friction of the air, but it should be noted that in some cases its influence can be decisive, especially when it comes to distant shots or when wind blows.
The parabolic motion is analyzed by decomposing it into two motions: a horizontal one, which is equivalent to the uniform rectilinear motion that we saw in the case of the penalty, and a vertical one, which, due to the force of gravity, is represented as an uniformly accelerated rectilinear motion. So, to evaluate the horizontal motion we will use the well-known equation (1): X = Xi + Vx.t (where the suffix in Vx is specifying that it is the horizontal
component of the velocity), but this equation will not work for the description of the vertical motion, since we must take into account the uniform acceleration due to the action of the gravitational attraction that the ball suffers throughout its trajectory.
For vertical movement we will need two more equations:
(2) Y = Yi + Vyi.t + ½.g.t²
(3) Vy = Vyi + g.t
Where:
- Y and Yi represent the vertical position of the ball at a given time and at the initial instant respectively.
- Vy and Vyi represents the vertical velocity of the ball at a given time and at the initial instant respectively.
- t is the time.
- g is the acceleration of gravity. In the terrestrial surface it is a constant equivalent to -9,81 m / s².
The parabola that the ball will describe will depend only on the force and angle at which it is propelled. Suppose that it is kicked with an initial velocity (Vi) of 45 km / h (equivalent to 12.5 m /s) with an angle of 30º with respect to the floor. With these and using the three equations that we have seen we can define how far the ball will touch the floor again, what will be the maximum height it will reach, how long it will take to do it, etc. Let's see how.
The first thing we must do is decompose the initial velocity (Vi) into its horizontal component, which as we saw is a constant (Vx) and its vertical component (Vyi). This is solved with basic knowledge of trigonometry:
Vx = 12.5 m / s. cos 30º = 12.5 m / s .0,8660254 = 10.8253175 m/s
Vyi = 12.5 m / s. sin 30º = 12.5 m / s. 0.5 = 6.25 m/s
Now let's work on the vertical component. Let's first determine the time it will take the ball to reach its maximum height. This is solved in a simple way considering that at that moment Vy will be equal to zero.
Then using equation (3): 0 = 6.25 m / s - 9.81 m/s². t
We cleared t:
t = (-6.25 m / s) / (-9.81 m / s²) = 0.6371 s
Placing this result in equation (2) and solving we can determine the maximum height reached by the ball: 1.99 m.
And placing it in equation (1) and solving we will obtain the horizontal distance (that is, with respect to the playing field) that will have reached at that moment: 6.8968 m; that being a parabola is half the distance, so, twice that distance will be the distance at which the ball would touch the ground again: 13.7936 m.
Direct Curling Free Kick (Screw Shot)
So far we have analyzed the trajectories of the ball without considering it as a sphere with dimensions, but we have treated it as if it were a point. However, for what comes next we can’t do that simplification. From now we must pay attention to the fact that the ball is a sphere and as such, in addition to the movement of translation that we studied so far, it´s susceptible to rotate, that is, to describe a circular movement around its own axis.
In the free kicks the ball must overcome a wall of men formed by the opposing team at a certain distance from the place of execution: not less than 9,15 meters according to the regulations of the game. Now, if the player wanted to use gravity simply to get the ball over the wall and then fall into the goal, the shot probably would not bring too many complications to the goalkeeper.
If the free kick is in the immediate vicinity of the area, then the wall will be the main obstacle for the kicker to disturb the goalkeeper. If we simply use the laws of the parabola, given the short distance of travel, the ball should be driven with little speed so that it could overcome the wall and fall back under the crossbar.
When the free kick is far from the goal, the wall itself is no longer an important obstacle (in fact, depending on the case, it can be considered unnecessary to form it or sometimes it is reduced to a single player), but the distance itself.
Making use of the equations of the parabolic motion we can determine what distance from the playing field would need to travel a ball that was kicked with an initial speed of 28 m/s (as in the penalty) and that at 9.15 meters of horizontal distance should reach a height of about 2.2 meters (and perhaps we are short considering that the players of the wall can jump to cover more height and also that the ball has dimensions), to fall back to a lower height than the goal (2.44 m). The calculations (the interested reader can corroborate it by itself) lead us to define that we must kick with an angle of approximately 17º and that the ball will go back down to the height of the goal about 35 meters away.
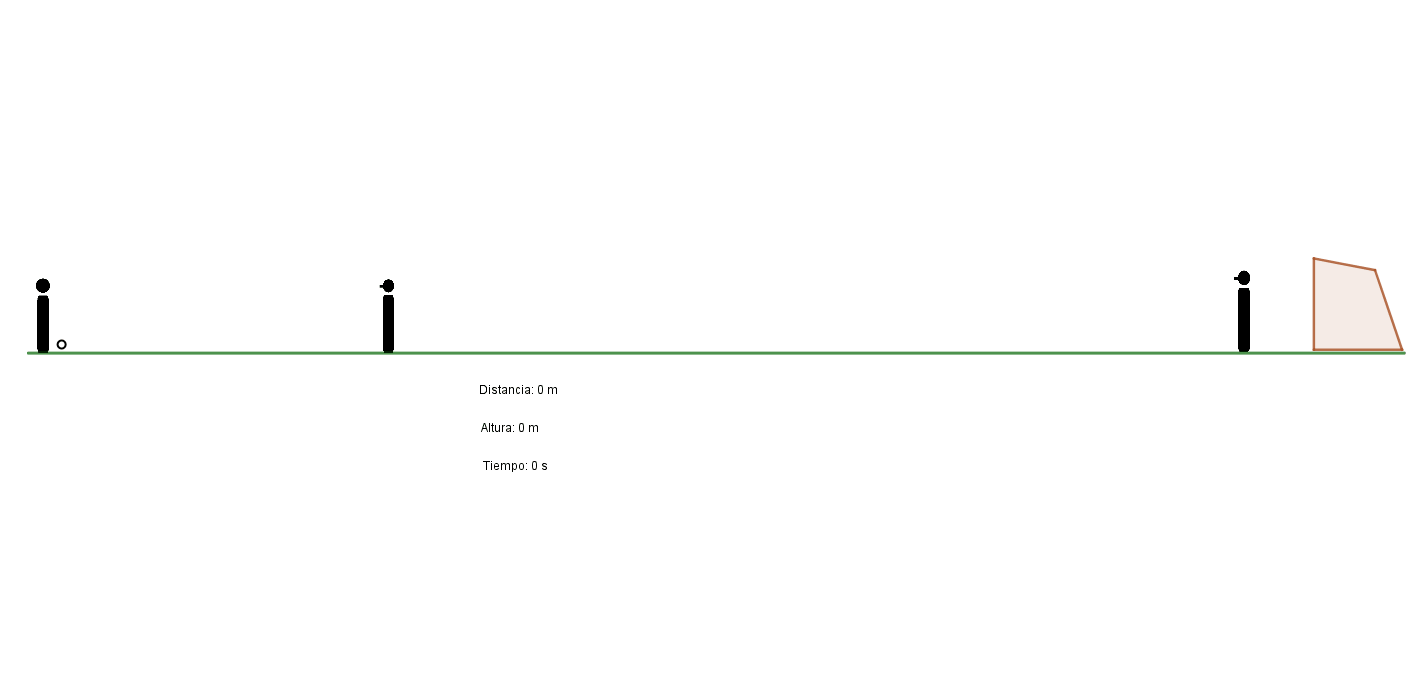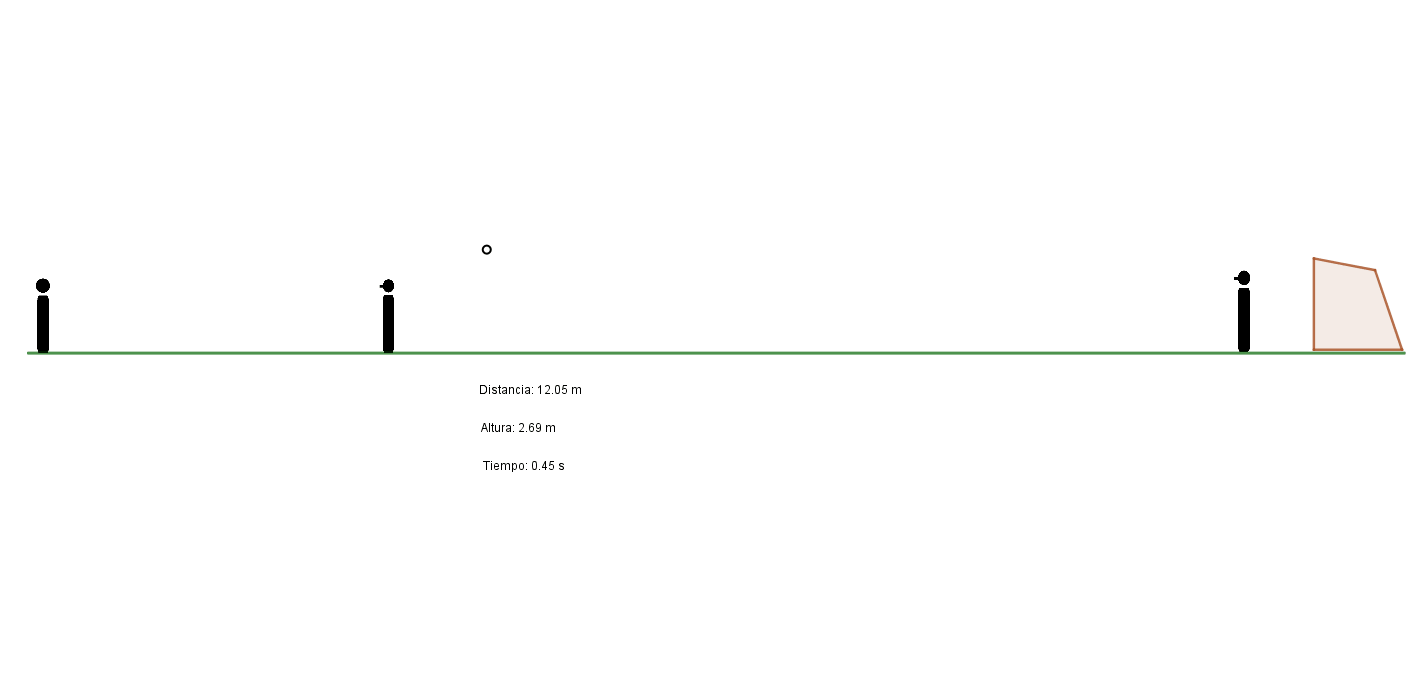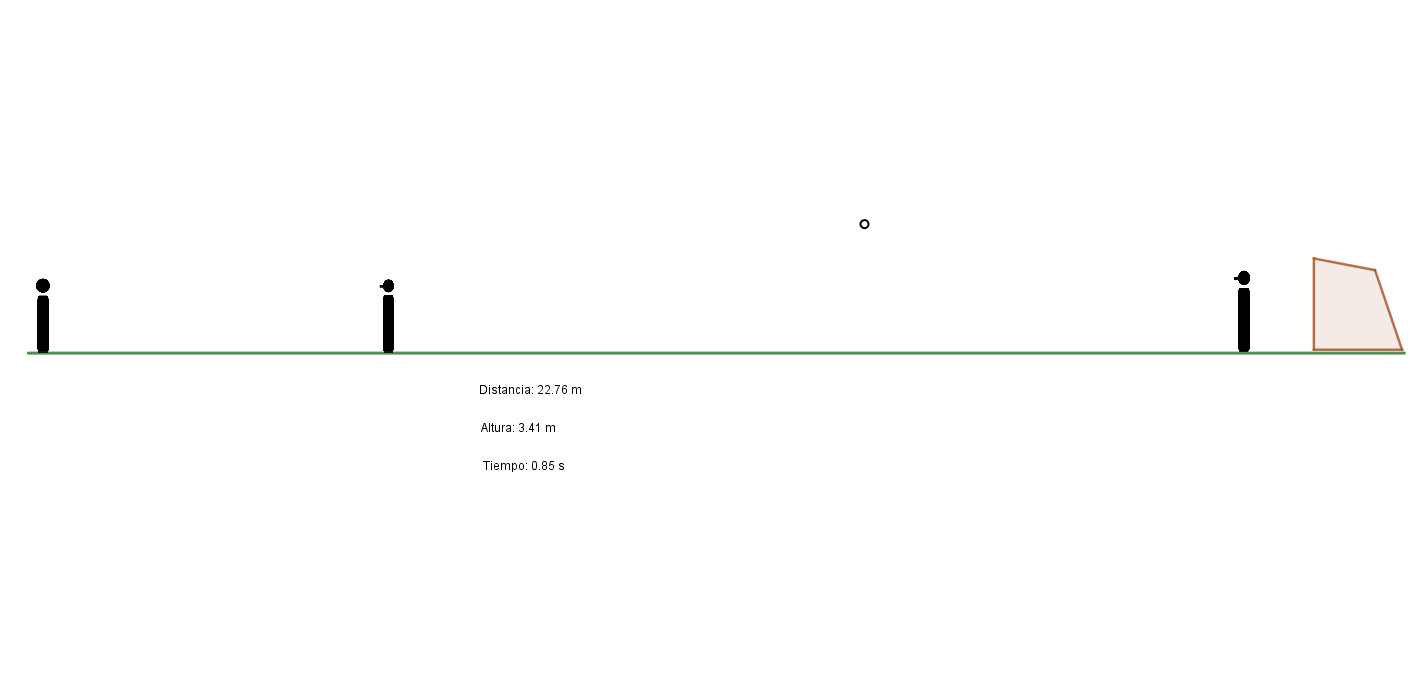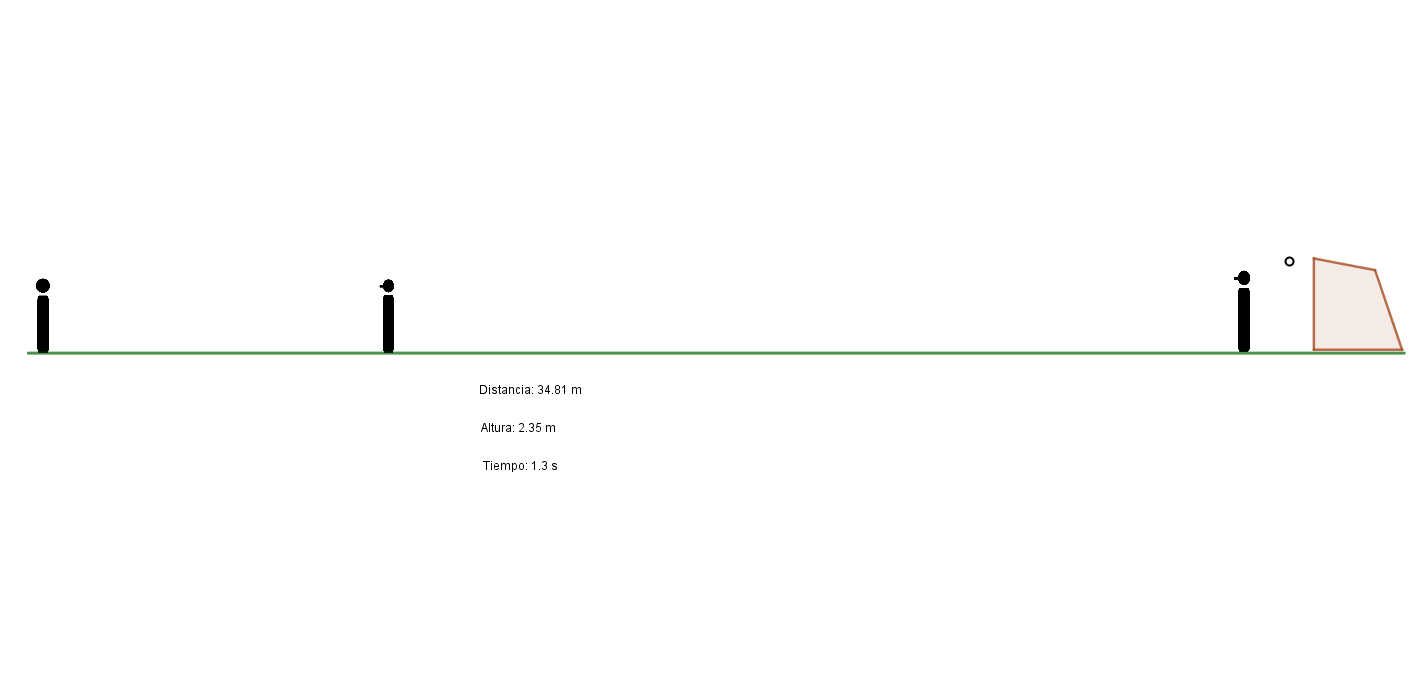
That is to say that for a free kick to succeed after avoiding a wall from above, it seems that it must be executed from a minimum distance of 35 meters from the goal. Then, how do expert executors make free kick goals at a shorter distance? They simply resort to another law of physics that, as we shall see, is closely related to the flight of aircraft.
Mechanics of Fluids
What makes planes fly? (Bernoulli Effect)
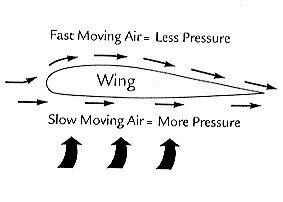
The secret for a plane to fly is in its aerodynamic design that largely involves its wings. If you look at the wing of an airplane, you will see that the top is curved while the bottom is almost flat.
Here intervenes the Bernoulli Effect, which arises from the branch of physics that studies the mechanics of fluids. Basically it says that in a moving fluid (such as air from the perspective of a moving plane), the sum of the pressure and velocity at any point will remain constant. So if you increase the speed should decrease the pressure and vice versa.
The shape of the airplane’s wing (airfoil) causes the laminar air flow lines to be squeezed at the top of the wing. So it travels faster at the top than at the bottom. Then, according to Bernoulli's principle, the pressure above the wing should be less than below. This pressure difference produces a resultant that pushes the wing up (ie, from the area of higher pressure to the area of least pressure).
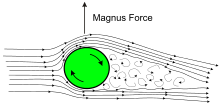
What causes the curl of the ball? (Magnus effect)
Let's see now that a ball that moves through the air while it rotates suffers a pressure difference on different sides of its surface. But how does this happen if, unlike the wing of the plane, the ball is symmetrical?
What happens with the spinning ball is that it tends to brake the air that crosses it on the side whose direction of rotation coincides with that of translation of the ball (and therefore opposes the sense of air flow), while accelerating the air that crosses it from the opposite side. So there is again a difference in velocities in the fluid and consequently, by the Bernoulli principle, a difference in pressure.
Thus, in a free kick the player will try to kick the ball so that it comes out rotating. If the intention is to overcome the wall above, then he must achieve that the direction of the rotation movement of the upper side coincides with that of the translation of the ball. Then up the air will lose speed (higher pressure) and lower will increase (lower pressure), resulting in a push down (from the area of higher pressure to the lower pressure).
Soccer has also taught us excellent executions in which the wall was overcome by the side, making the ball spin with its axis perpendicular to the floor. And of course not only in the free kicks you could see executions that use the Magnus Effect.
Instep Kick (Drag Force)
Whoever has seen enough football will have been able to observe some shots in which the player hits the ball in such a way that it goes straight, and yet, before reaching the goal, the ball sometimes surprises the goalkeeper with a short and sudden movement to one of the sides. This is already a much more subtle question in which the luck factor intervenes. Neither the kicker nor the goalkeeper can foresee such minimal and surprising movements of the ball. As happened to the Uruguayan goalkeeper, Muslera, in the match his team lost to France in the quarterfinals of the cup.Muslera’s declaration
But what causes these sudden and unpredictable movements? First of all I must confess that unlike the rest of the cases discussed here I did not find in the bibliography that I consulted an explanation to this particular case. However, everything seems to indicate that here is relevant the influence of a force that until now we have left aside because it is considered negligible: the drag force.
When a ball travels through the air it tends to decelerate due to the friction with the fluid itself. That is to say, there is a force acting on the ball in the opposite direction to that of its movement.
Now, one would expect in principle that this force will simply constantly hold the ball down without altering its trajectory. But a solid object when rubbing with a fluid does not behave the same as in friction with solid surfaces.
Laminar flow and turbulent flow
The mechanics of the fluids distinguishes two possible states of flow: * laminar *, when the flow moves in an orderly manner, and * turbulent *, when its motion is disordered. The variable that defines the state of the flow is the speed of its movement. If a laminar flow is increased speed will sooner or later reach a critical point where it will become turbulent, and vice versa.
It is worth mentioning that the Magnus Effect indicated is when the flow is laminar (ordered). When the flow is turbulent this effect is quite diminished. In addition, the drag force that tends to slow down the movement of the ball is quite minor when the flow is turbulent. Then, a ball that moves faster than the critic is diminished the interference of the air that crosses over it.
In principle this does not seem to bring more news. Previously we have analyzed the parabolic motion where even for lower speeds we have considered negligible the influence of drag forces and now we are saying that for the case of movements in a turbulent state these forces are even more negligible. That is unquestionable. But what would happen if during the flight of the ball to the goal it passes from a turbulent state to a laminar state?
It can be thought that when a ball is kicked with enough force, it can be fired with such speed that its movement is turbulent. Then both the drag force and the Magnus Effect would be acting very weakly. But that the resistance is weak does not mean that it does not exist. If the critical point is close to the speed reached, the air resistance may be sufficient for the ball to fall below it before reaching the goal. Then the flight of the ball would become laminar, which would cause it to experience a sudden change in both its speed (decrease due to the increase in drag force) and in direction (due to a greater incidence of the Magnus Effect), if the ball has a certain spin (rotation). This can be an explanation of what happened in Griezmann's goal to Uruguay.
The ball and the perfect sphere
An alternative explanation could be given if we consider that soccer balls are not perfect spheres.The balls have segments (hexagons and pentagons), in addition to a peak where it is inflated. These "imperfections" of the ball would cause that the airflow is not all the laminar that is expected in a perfect sphere, which could lead to a behavior of the ball less predictable.
It should be noted that this alternative explanation seems to respond better to the type of shot that we are evaluating, given that it would occur first of all in those executions in which the ball does not rotate or its rotation is minimal. And it is that when the ball rotates quickly the constitutive imbalances of the ball swing, making it more like a perfect sphere. In fact, some goalkeepers have complained in particular about the ball used in the World Cup. Goalkeepers complains
So which of these two hypotheses can be used to explain Griezmann's goal to Muslera? Video Perhaps there has been a fortunate (or unfortunate) combination of both.
Energy (Impact)
In order to finish this work we will make some considerations referred to the impact of the ball by the foot of the soccer player.
When the ball is hit by the player's foot, it is deformed, compressed. This understanding is the product of the impact of the foot on the ball and is the way in which the ball receives the energy that our foot transmits to it during the impact. The ball at that moment acquires potential elastic energy, is equivalent to thinking of a spring that is compressed. When the ball (the spring) is released from that compression and, consequently, goes off, that potential energy has become kinetic energy.
When a ball instead of being initially at rest is moving towards the foot, then it already brings a kinetic energy that enters the equation at the moment of impact to transform into elastic power energy, so that even if the foot applies the same force on the ball, the compression of the ball is greater and when bouncing it will leave with greater speed.
The same happens when the impact surface is smaller, as in a toe kick, then the ball is compressed more. This is a resource that scorers can use when they are in a situation in which the path of the foot to hit the ball is short, then a toe kick is helpful to print more speed to the ball. Of course, as power is gained, accuracy is lost in the execution, with which it is generally preferred to hit the ball with the inside face of the foot, the outside or the instep.
[1] The graphics were done by me with the GeoGebra program.
[2] In this context we call it force, since we are in the framework of Newtonian Mechanics. On the other hand, General Relativity no longer considers gravity as a force, but as a curvature of Space-Time.
Bibliography
Books:
- Young H., Sears F.W., Freedman R., Zemansky M.W. (2009) Física Universitaria (Volumen 1), Mexico: Pearson Education.