The field equations of general relativity
Einstein used several years and many discussions and works with mathematicians, especially Marcel Grossman and David Hilbert, in order to achieve the mathematical expression of his ideas. Although Einstein already had a first draft in 1911 it would not be until the end of 1915 that he found the definitive form [3]. The field equations were presented to the Prussian Academy of Sciences in November 1915. The general idea is that the solutions to these equations indicate how spacetime and mass-energy influence one another and vice versa. For example, how spacetime affects the presence of a mass like the Sun, and how this spacetime affects the movement of a smaller mass in the vicinity of the Sun, like that of a planet; or what happens to spacetime when a massive star collapses on itself to create a point of infinite density.
The mathematical difficulty that Einstein found is to express quantitatively that spacetime is curved and how it does it. To achieve this he had to learn the basics of a whole branch of mathematics: the tensor calculation.
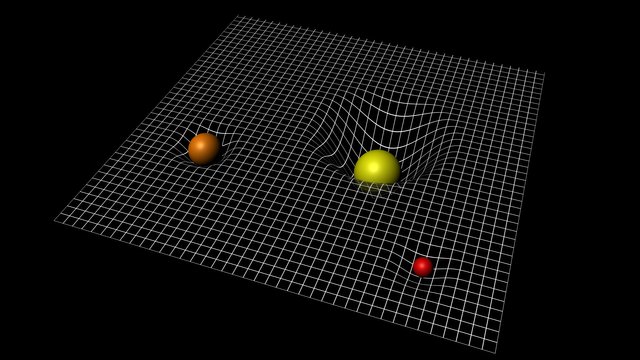
Spacetime is curved in the presence of mass-energy. Image: ESA-C.Carreau
Spacetime can be curved
If you cut an orange in half, you remove the pulp inside, and try to flatten the resulting hemisphere of skin, you end up cracking it. If you try to flatten something in the shape of a saddle, like a fried potato (of the bag), you find the opposite problem: there is "too much" surface and you form folds. If you take, however, a roll of kitchen paper and you want to flatten it, there is nothing easier, with unrolling it, ready. Surfaces such as spheres are said to be positively curved, those that have the shape of a saddle that are negatively shaped, and those that are like kitchen paper are simply flat (let's realize that they are flat in this sense). although they are not in a plane). This is so because the curvature is defined in terms of "intrinsic geometry" of a surface, in which the distance is measured as a function of the paths that are within the surface.
There are several ways to make this notion of curvature precise and to make it quantitative, in such a way that at each point on the surface a number can be associated that says "how curved" is at that point. To be able to do this it is necessary that certain mathematical conditions are met that allow determining the lengths of the roads, this is what is called a Riemannian metric. The notion of curvature can be generalized to a greater number of dimensions, in such a way that we speak of the curvature at a point in a Riemannian variety of d dimensions. However, when the dimension is greater than two, that is, it is not a plane that is curved but a space, the possibilities of curvature at a point become so complicated that they can no longer be expressed by a number but by something called the tensor of Ricci.
A tensor is simply the extension of the vector concept to additional dimensions. A scalar, a number, appears in a graph as a point, a zero-dimensional object. A vector, which has magnitude and direction, would appear in a graph as a line, that is, as an object of a dimension. The tensioner extends this idea to the additional dimensions. This can be interpreted as a set of related vectors, moving in multiple directions in a plane.
We will see it better in another way. Instead of thinking of a vector as a set of coordinates, we can consider it an operation, that is, a vector what it would do is to associate an address with a number. The important thing from the mathematical point of view is that the operation is linear and homogeneous. Thanks to this, a vector is completely determined by its projections in d directions, where d is the number of dimensions of the space in which it is defined. Therefore, a vector can be expressed as a set of numbers that are actually its projections in a system of coordinate axes.
A vector is really a tensor of rank 1, associates 1 direction to a number. A scalar, is a tensor of rank 0, associates 0 directions to a number. Therefore a tensor of rank 2 (a tensor already by own right), associates two arbitrary directions to a number. If we wanted to express it in terms of coordinates, as it is done with vectors, we would need d x d numbers. For a tensor of rank q, therefore, we would need nq numbers.
The field equations
Let us now look at the field equations of general relativity from the formal point of view. If you have arrived reading this far it will not scare you too much, after all it is nothing more than a tensor equality in which a set of 4 x 4 tensioners are related (symmetrical, but in this we are not going to enter now), for a spacetime of 4 dimensions
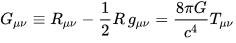
Where Rμν is the curvature tensor of Ricci of which we spoke above, R is the scalar curvature (simplifying, the curvature understood in the sense we spoke above, a number associated with a point in space), gμν is the metric tensor ( a generalization of the gravitational field and main object of interest), G is Newton's gravitational constant, c the speed of light in vacuum and Tμν the energy-impulse tensor.
The indexes on the tensors are labels, it's a way of calling them. In this case Penrose's abstract notation is used. Any convenient symbol for indexes of tensioners can be used. Traditionally, Latin letters are used to indicate that spatial coordinates are being used (x, y, z), while Greek letters are used to indicate spatial-temporal coordinates (x, y, z, t).
Notes:
[1] This installment of the series can be skipped without loss of continuity.
[2] In what follows we rely mostly on our our "Einstein and ... the slate of Mount Wilson Observatory" Experientia docet 12/17/2010
[3] The importance of chronology can be seen in our Deviation of light and falsifiability
About the author: César Tomé López is a scientific disseminator and editor of Mapping Ignorance