What happens when an irresistible force meets an immovable object? Which superhero will win a fight?

• Can Wolverine take batman?
• Incredible Hulk vs the Thing?
• Superman vs Wonder woman?

These kinds of topic are in line with what we want to tackle now. What we’re really concern is whether one infinite set is bigger than another, or is they the same size.

Three reasons why people disdain to consider such question:

1. Like superheroes, infinite sets are just products of human-imagination
2. There can be no difference because “infinite is infinite”
3. This are not going to earn me big piles of money so “who cares?”

Point 1:

To physicists, we are living a finite scope of the universe, containing a finite number of subatomic particles, so in reality there can be no infinite sets.

However, in the field of mathematics, some axioms consider the assumption that the objects of consideration are indeed infinite in number. Infinity basically boils down to being just a concept.

Point 2:

When we think of the size of infinity we think “there’s only one size of infinity”. This argument is wrong! There is actually a informal argument showing that there are at least two sizes of infinity, and what’s even crazier is that there is a formal theorem that shows there is actually an infinite hierarchy of infinities.

Point 3:

“who cares?” is the toughest of all to deal with. But, hopefully, you enjoy clever arguments for their own intrinsic beauty.

Let’s get started

1. Which set is bigger – the natural numbers, 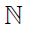or 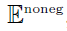, the set of nonnegative even numbers?

---

Intuitive answers (that are wrong in some sense.)

initial answer: both are clearly infinite so both are of the same size? This may lead to the correct answer but through some invalid reasoning.

another answer: even numbers are contained in the natural numbers so somehow even numbers are smaller than the naturals.

Right answer using valid reasoning:

Here’s how we do it. Remember how Cantor defined one-to-one correspondence,

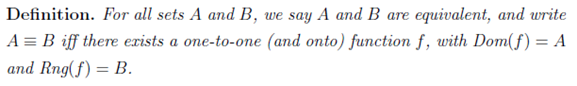
To show that two sets are of the same cardinality, we show that both sets follow the one-to-one correspondence. What we need now is a way:

1. Pair an even number to a natural: given some non-negative even number e we need to come up with an x such that
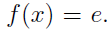
2. Given a natural how can we produce an even number to pair with it
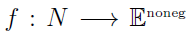   defined by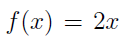

By definition of an even number, there exist a k such that, 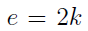and since k is either 0 or some positive number it follows that k is actually the x we are searching for. The set of k’s belong to the set of the naturals,

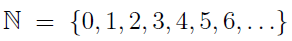
Put more succinctly, every non-negative even number 2k has a preimage, k, under the map f, thus f maps the naturals surjectively onto even positive numbers. And so,

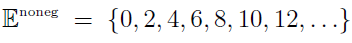
In principle, both sets can be listed as.

2. Which set is bigger – the natural numbers, 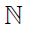or the set 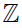of integer numbers?

---

Note that integer numbers are usually listed with dot-dot-dots forward and backward,

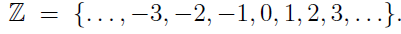
One way to simplify this is to list the integers in a singly infinite set using symbols, which then show that the integers are actually equinumerous,

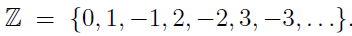
This set allows us to list a one-to-one correspondence with - first entry corresponded with 0,the second entry is paired with 1, the third entry is paired with -1 and so on,

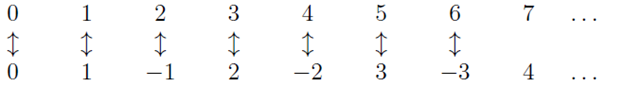
In fact, any singly infinite listing can be thought of as displaying a one-to-one correspondence with .

Notice that the negative numbers are paired with even naturals and the positive integers are all paired with odd naturals. This leads us to a piecewise definition for a function that gives the bijection we seek,

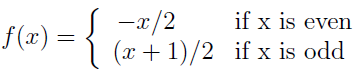
What we’ve shown so far are the cardinalities of natural numbers with even naturals, and natural numbers with integers. We found that they all have the same cardinality. This first cardinal number is known as the 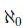(sets having the same cardinality with the natural numbers). In some sense, we could view both the equivalences we’ve shown as demonstrating that ,

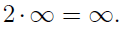3. What is the cardinality of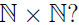

---

You can visualize the set 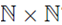as the points having integer coordinates in the first quadrant

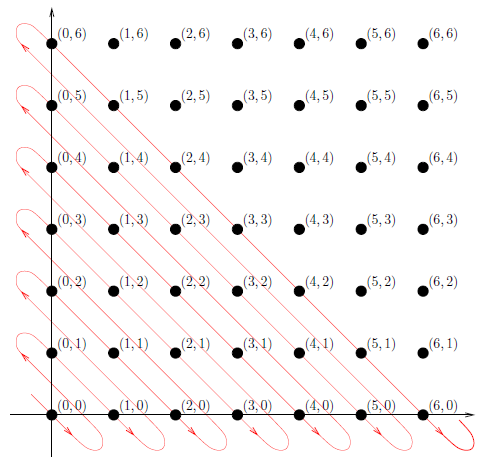
This set of points and the path through them is known as the Cantor’s snake. This diagram gives us a visual form of the one-to-one correspondence we seek. In tabular form,

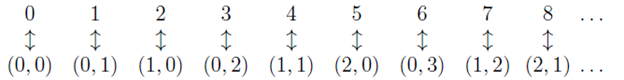
Just like what we did before we need a mapping:

1. From the pairs 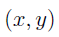back to the naturals n.
   The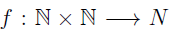 is defined as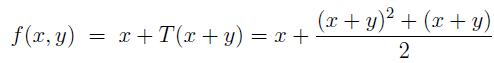
2. From the natural number n to the pairs
   

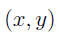
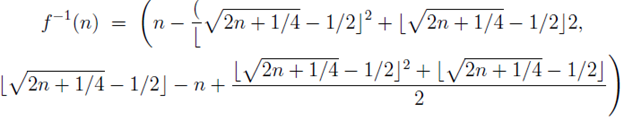
Given some restrictions appropriate to the sets, these two functions are two-sided inverses for one another. This implies that f is bijective.

Summary:

---

We have shown that the sets 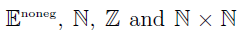all have the same cardinality - .

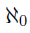^{Disclaimer: this is a summary of section 8.2 from the book A Gentle Introduction to the Art of Mathematics: by Joe Fields, the content apart from rephrasing is identical, most of the equations are screenshots of the book and the same examples are treated.}

1. A Gentle Introduction to the Art of Mathematics by Joe Field

---

Thank you for reading ...