[수학]Zorn's lemma, 선택공리, 그리고 well-ordering principle 소개

오늘은 Zorn's lemma 의 응용에 관한 문제를 소개해 볼까 한다. 의 다양한 동치 표현에 대해서 소개해 보려고 한다.

일단 Zorn's lemma 에 관해서 프렐라이의 현대대수학 책[가장 널리 쓰이는 교재, 요새는 Hungerford 나 Dummit 에 밀리는 중...] 에서는 다음과 같이 언급한다.

Axiom of choice 와 Zorn's lemma 그리고 well ordering principle 은 대수학, 집합론, 위상수학에서 공리로 생각하는 것 중 하나이다. 희한한 것은 이 세 개는 서로 동치 관계이다는 거 하나 하나는 증명할 수 없지만 하나를 통해서 다른 하나를 증명하는 것은 가능하다.

마치 Triality 처럼 ㅎㅎ

학부 위상수학 수업이었나 저 3가지가 서로가 서로를 implies 하는 것을 보이는 문제가 숙제로 나왔었고 그 때 고생을 좀 했던게 기억이 난다. ㅋㅋㅋ 그렇게 힘들게(?) 공부했는데 지금 머릿속에는 남지가 않는군...

---

오늘 이 포스팅에서는 Zorn's lemma 에 대한 간략한 설명과 대수학과 관련되서 이 Zorn's lemma 의 3가지 application 에 대해 다루어 보려고 했다.

바로

이 3가지를 증명하는데 Zorn's lemma 는 아주 유용하게 쓰인다. [특히 infinite set 을 다룰 때 그 무한대 집합에서 크기를 다룰 때 유용하게 쓰인다!!!]

흠 아무래도 이 3가지 증명은 다음 기회로 미루어야 될 것 같다. [ㅠㅠ]

저 위의 3가지 공리들에 대해서 간략히 소개 정도만 해보자

Zorn's lemma

Let S be a non-empty poset. If every chain C in S has a upper bound in S, then S has a maximal element

Zorn's lemma 를 제대로 이해하기 위해서는 poset 즉 partially ordered set 에 대해서 알아야 하고, chain 과 upper bound, maximal element 의 정의에 대해서 생각해 보아야 한다.

일단 set 에 order 라는 것이 무엇이냐고 한다면 숫자는 크기라는 기준을 쉽게 생각할 수 있지만 set 에서는 그 크기라는 개념이 애매하다. set 의 원소의 갯수를 기준으로 한다거나, set 의 원소중 가장 큰 숫자 를 기준으로 하거나.. 등등 정의할 수 있는데 일반적으로 set theory 에서 order 를 inclusion 으로 정의한다.

무슨 말이냐 하냐면 부분집합을 가지고 order 를 표현한다는 것으로 A={1,2} 이고 B={1,2,3} 이면 B 가 A 를 포함하기에 B 가 A 보다 크다(?) 라고 표현한다는 것이다. (엄밀하게는 포함한다를 가지고 ordering 을 표현한다)

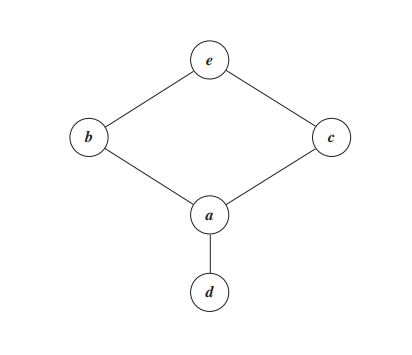
Chain 이라는 것은 흔히 생각하는

의 수학적 추상화로 이를 표현한 diagram 을 Hasse diagram 이라고 한다.

upper bound 나 maximal 은 우리가 직관적으로 생각하는 그 정의가 맞다.

즉 maximal element x in S 라는 것은 집합 S 의 maximal 원소은 x 보다 큰 원소가 없다는 것을 의미하고 upper bound 의 경우 어떤 임의의 원소 x(S 에 속할 필요가 없다) 보다 S 의 모든 원소는 작거나 같다라는 것을 의미한다.

재밌는 것은 이 maximal element 는 upper bound 가 될 필요가 없다는 것이다.
( In a poset, an upper bound is a maximal element but the reverse is not generally true! )

또 더 재밌는 것을 생각할 수 있는데 maximal 원소와 greatest 원소를 구별할 수 있다는 거.. 사실 영어적 해석을 하면 별 차이가 없어 보이지만 수학적 정의에서는 partial order 와 linear order의 차이로 이런 일들이 일어난다... (이런 partially order 와 linear order 의 정의를 설명해야 하는데 이러면 binary relation 을 설명해야 되고 또 산으로 가서 편의상 생략했다...)

Axiom of choice

Let C be a collection of nonempty sets. Then we can choose a member from each set in that collection

이것은 우리말로 선택공리라고 하는데 논리학에서도 자주 등장하는 그 공리이다.

사실 집합이 유한개의 원소를 가지고 있다면 이는 지극히 자명하지만, 갯수가 무한개가 되면 .....

선택 공리의 가장 큰 장점은 이 것으로 인해 무한 집합의 경우에도 cardinality 를 정의 할 수 있다는 것이고, 또 무한 집합 사이의 크기 비교를 할 수 있다는 것이다.

오 이런 나무위키에 이런 항목이 있었네?

진작 좀 찾아볼껄 ㅋㅋㅋ 여기서 ZF 는 체르멜로-프렝켈 집합론을 말하는데.. ㅋㅋㅋㅋ 이런 detail 은 수리논리학 과 같은 수업 시간에 배울 수 있다. [이름만 들어보고 사실 나는 거의 알지 못한다 ㅠㅠ]

공리계에 대해서 예전에 한번 공부해 볼까 했는데 ㅋㅋㅋㅋㅋ
지금도 그렇고 아직도 버겁군 ㅋㅋㅋㅋ

나무위키만 봐도

ㅋㅋㅋ 위상수학의 separable axioms 의 악몽이 떠오른다 ㅋㅋㅋㅋㅋ

관심있으신 분이 쉽게 보시라고 나무위키 링크를 걸어놨다. ZFC 공리계

수리논리학 이것도 언제 한번 공부해 보고 싶은데 ㅋㅋㅋㅋ
알고 싶은게 너무나 많아 걱정이다

Well ordering principle

every non-empty set of positive integers contains a least element.

ㅋㅋㅋㅋ 사실 난 이게 가장 직관적이라고 생각했는데

Well Ordering Principle is contrary to the intuition of most mathematicians

이런 ㅋㅋㅋㅋ

사실 Well ordering principle 의 개념은 고등학교 때 배우는 수학적 귀납법과 같다. 다시 말해 every non-empty set of positive integers contains a least element. 이 것을 수학적 귀납법으로 증명 할 수 있다는 것이다. ㅋㅋㅋ 아무래도 선입견이라는게 있어서 제일 먼저 이 공리를 접해 너무나 자연스럽게 여겨졌나 보다.

well ordering principle 을 수학적 귀납법으로 증명하는 과정은 다음의 자료 를 참고하면 된다.

사실 이 문제는 종종 Homework 나 시험으로 출제되기도 한다.

---

Axiom of choice 관련하여 조금 더 끄적여 보자.

일단 관련 자료[역사적 혹은 그 논란의 이유 등]의 한 사이트 에서 한 문단을 가져와 본다.

Jerry Bona once said,
The Axiom of Choice is obviously true; the Well Ordering Principle is obviously false; and who can tell about Zorn's Lemma?

This is a joke. In the setting of ordinary set theory, "all three of those principles are mathematically equivalent" -- i.e., if we assume any one of those principles, we can use it to prove the other two. However, human intuition does not always follow what is mathematically correct. "The Axiom of Choice agrees with the intuition of most mathematicians; the Well Ordering Principle is contrary to the intuition of most mathematicians; and Zorn's Lemma is so complicated that most mathematicians are not able to form any intuitive opinion about it."

즉 Axiom of choice (선택공리) 가 가장 직관적이고 Well ordering principle 이 가장 직관에 반대되고 Zorn's Lemma 는 복잡하다 이건데 ㅋㅋㅋ

아무래도 정규 교육 과정 중에 대부분 거꾸로 배워서 Well ordering 이 가장 쉽게 느껴지고, Axiom of choice 는 뜬구름 같고, Zorn's lemma 는 그냥 복잡하다 이건가? ㅋㅋㅋㅋ

이 세 공리(?) 정리(?) 가 동치인것을 보이는 것은 종종 point-set topology 에서 숙제 혹은 시험으로 잘 출제가 된다. 역시 수학은 배운지 오래되면 계산 방법만 기억이 남고 이런 정의, 정리와 그 증명들은 ... ㅠㅠ 사실 증명도 어떻게 보면 기교인데, 기교를 덜 닦다 보니 ㅠㅠ [예전엔 어떻게 했나 몰라 ㅋㅋ 결국 자기 세부 전공 아니면 다 까먹는건가..... 그래서 교수들에게 강의를 의무적으로 하게 하는 건가, 복습 하라고 ㅋㅋㅋㅋ ;;]

여하튼 시간을 내서 날을 다시 세울 수 있도록 시도(?) 노력(?) 해야 겠다.