선형보간법에 대한 간단한 이해

---

• 출처 : 선형 보간법 https://ko.wikipedia.org/wiki/선형_보간법

---

오늘은 간단히 선형보간법에 대한 이야기를 해볼까 합니다. 수학공식으로 디테일적으로 설명 하면 좋지만 그 내요은 위키백과에 위 링크된 위치로 가시면 선형 보간법에 대해서 잘 나왔기 때문에 굳이 반복해서 설명한 필요가 없고 최대한 간단히 잡이야기로 의미만 전달하는 내용을 담아 보았습니다.

선형보간법

---

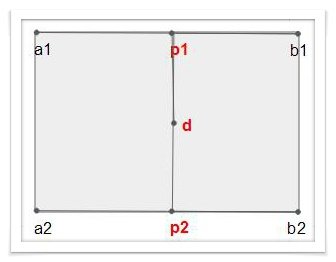
선형보간법이란 두 꼭지점 값을 기준으로 직선 상에서 이루어지는 보간법입니다.

위 그림과 같이 두 a,b의 값을 보간하여 특정 p위치의 값을 구하게 됩니다. 이 경우는 직선 상의 특정 위치의 꼭지점을 구하는 방식으로 1차 선형 보간법입니다.

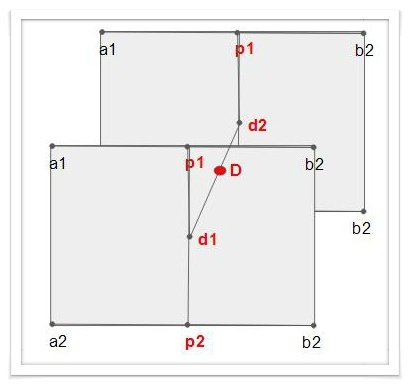
그 다음으로 두 직선상의 보간법으로 구한 꼭지점에서 특정 위치의 꼭지점을 구하는 방식을 2차 선형 보간법이라고 합니다.

이 방식은 두개의 직선 상의 p1과 p2라는 꼭지점이 구해지면 다시 p1과 p2라는 끝점을 기준으로 다시 d라는 꼭지점을 구할 수 있습니다.

그러면 다시 두 평면에서 구한 꼭지점을 기준으로 특정 위치의 꼭지점을 구하는 방식을 3차 선형 보간법이 되겠죠.

위 그림에서 보는 것처럼 평면 상의 꼭지점 d1, d2를 기준으로 다시 3차 선형 보간을 통해서 최종정적으로 D라는 꼭지점 값을 구할 수 있겠죠.

정리하면 1차 직선상의 꼭지점 p을 구하고 다시 두 p1, p2 위치에서 d를 구하고 다시 d1, d2 위치에서 D위치 값을 구하여 3D 좌표상의 꼭지점을 구하게 됩니다.

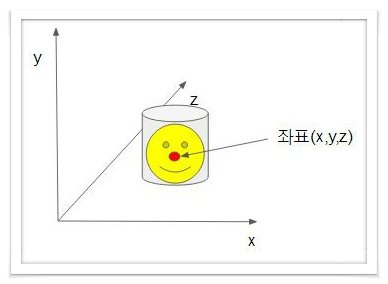
물체의 특정 위치값을 구할 때 선형 보간법을 이용합니다.

딸기코 같은 위치의 좌표가 선형보간법으로 이용하여 해당 위치 값을 구하여 물체의 색과 불투명도를 이용하여 3D 시각화를 할 수 있게 됩니다.

---

_{Sponsored ( Powered by dclick )}