퀴즈 523, 524, 525 풀이
퀴즈 523 9009
마지막 4자리가 9009로 끝나는 완전 제곱수 중에서 가장 작은 수를 찾아라
풀이
자 구하고자 하는 수를 x 라 하면 x^2 제곱의 끝의 4자리가 9009가 된다.
이는 즉 x^2 = 10000y + 9009 라는 것을 알 수 있다.
자 여기서 한가지 사전 지식이 필요하다.
바로 어떠한 제곱수의 끝이 9라는 것은 그 수는 3이나 7로 끝난다는 것이다.
[이는 trial and error 로 쉽게 보일 수 있다. 2의 거듭제곱은 2,4,8,6,2 로 계속 이 순환구조가 반복된다. 3의 거듭제곱은 3, 9, 7, 1, 3 으로 순환구조가 반복된다. 이를 반복해보면 3과 7의 경우만 짝수 제곱의 경우 끝자리가 9로 끝나는 경우가 존재한다는 것을 알 수 있다.
사실 이는 결국 어떠한 수들의 거듭제곱을 10으로 나눈 나머지를 보는 것이라, 합동식 개념을 알고 있으면 바로 보일 수 있다.]
끝자리가 3이나 7로 끝나니까 결국에 x =10a + 3 혹은 10a+7 이라는 것을 알 수 있다. 10a+7은 10a-3 꼴이랑 같으니 10a pm 3 형태가 되겠다.
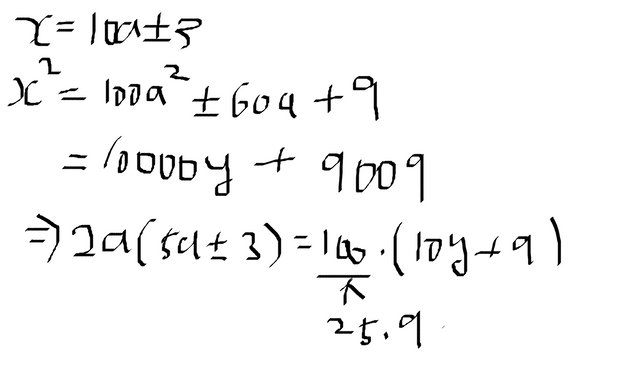
자 여기서 적어도 100이 등장한다. 근데 먼저 5a pm 3 은 5의 배수가 아니다. [5의 배수에 3을 더하거나 빼면 5의 배수가 아님] 이 말은 2a 가 5의 배수 더 나아가 25의 배수가 되야 한다는 것을 알 수 있다. [5a +3, 5a-3 은 5의 배수, 25의 배수도 아니다. 하지만 우변에 100이 등장함으로 a 는 적어도 25의 배수가 될 것이다.]
a=25b 라 하면
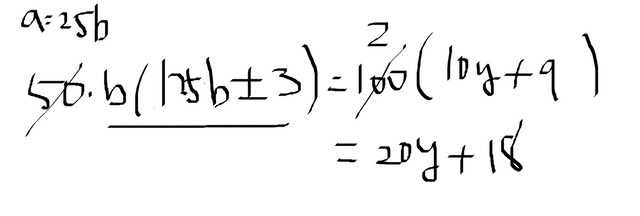
경우를 나누어 가장 작은 b 를 찾아보자. [일의 자리에서 찾으면 충분할 것이다.]
pm (plus minus) 의 경우를 나누어 고려한다.
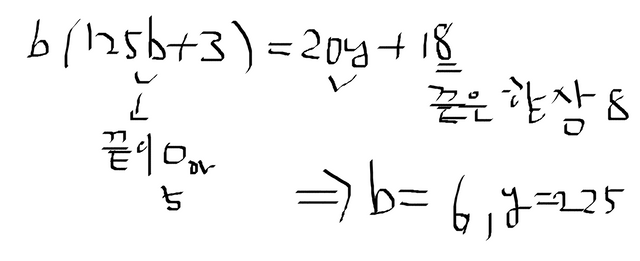
사실 b=1 부터 다 해봐도 된다. 먼저 끝이 8이 나오는 b 를 조합한 뒤 거기에 해당되는 y 값을 찾으면 된다. - 의 경우는 b=9 일때 y=504 가 나온다. 즉 b 가 6일때가 가장 작은 것을 알 수 있다. b=6 이면 x=250b+3 = 1503 이 되고 즉 x^2 = 22590009 가 된다.
퀴즈 524 필승전략6
이전의 필승전략, 그리고 NIM 게임 관련된 것의 일반화된 문제이다.
홀수개의 돌 무더기가 있다. 두 사람이 번갈아 바둑돌을 가져가는데 최소 a 개에서 최대 m 개 까지 마음대로 가져갈 수 있다.
테이블 위의 바둑돌이 모두 없어졌을 때 홀수개의 바둑돌을 가져간 사람이 이기는 것으로 했을 때, 누가 이길 수 있겠는가?
어떻게 하면 필승전략을 구사할 수 있을까?
풀이
홀짝성을 파악하면 쉽게 생각해 볼 수 있다. 상대가 가진 수가 짝수이면 상대방에게 2k(a+m) 개를 남겨 주고, 홀수이면, 2k(a+m) + a 개를 남겨주면 된다.
일반화가 어렵다면 숫자를 넣어보고 거꾸로 역산하면 이를 쉽게 생각할 수 있다.
퀴즈 525 정사각형 쪼개기
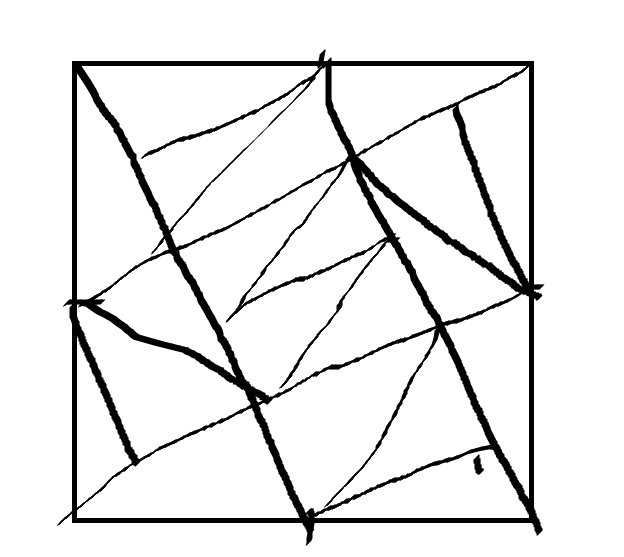
정사각형의 4변 어떤 변에도 평행하지 않게 선을 그어서 20개의 서로 합동인 도형을 만들어라
풀이
먼저 각 변의 중점을 자르고 선분을 그은 뒤 그려지는 삼각형에서 직사각형을 만들어 같은 크기의 삼각형으로 쪼개면 된다. 정사각형의 4변에는 평행하지 않지만, 그은 4개의 선은 2개, 2개씩은 서로 평행하고, 또 거기서 생기는 작은 삼각형을 모양으로 평행하게 선을 그어주면 된다.