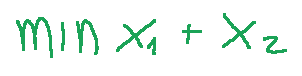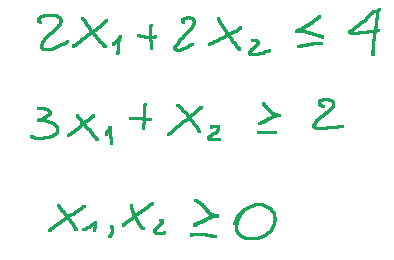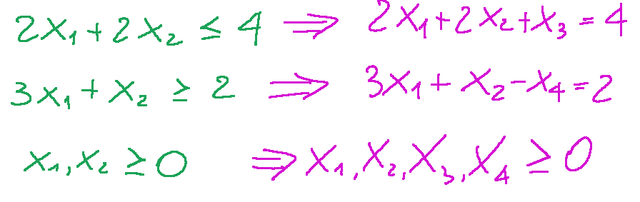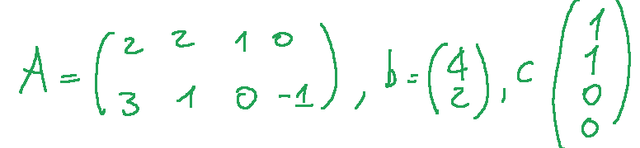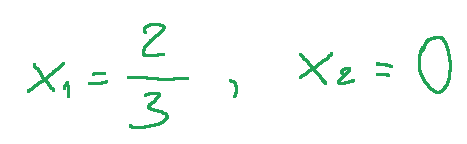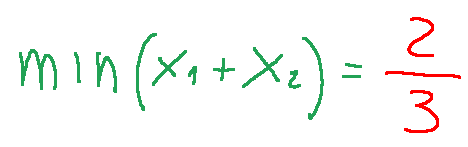04-11-2025 - Exercise - Description of a Linear Programming Exercise [EN]-[IT]
Cover background image generated with AI, software used: copilot microsoft
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
04-11-2025 - Exercise - Description of a Linear Programming Exercise [EN]-[IT]
With this post, I would like to provide some brief insights into the topic mentioned above by solving some exercises.
The context in which we operate is that of Operations Research
(lesson/article code: MS_14)
Linear Programming
Linear programming is an important subject of study for the industrial and transportation sectors. It is part of the even broader subject of Operations Research.
Exercise
Let's consider the following linear programming problem, which is a minimization problem.
This problem is subject to the following constraints:
Transformation to Standard Form
The first thing we need to do to continue with the exercise is convert it to what is called standard form.
To do this, we need to introduce the slack variables.
The introduction of slack variables helps us transform inequalities into equalities.
Below are the constraints transformed into standard form with slack variables (purple).
Constraints and variables
In standard form, the problem now has 2 constraints and 4 variables.
Various ways to solve the problem
To solve a linear programming problem, we can use the simplex method. The Simplex Method proceeds by generating a sequence of basic feasible solutions with a non-increasing objective function value, until the optimal solution is found or the problem is concluded to be unbounded.
For the problem described above, we can define the coefficient matrix (A), the vector of known terms (b), and the objective function coefficients (c).
To solve this problem, we can also use the Simplex Method (Phase 2). The goal of the Simplex Method (Phase 2) is to start from a basic feasible solution and iterate through pivot operations, swapping columns within and outside the base, until the optimality criteria are satisfied.
You can also use the graphical method, which constructs the polyhedron of solutions and finds the optimum at one of the vertices of the polyhedron.
For example, it has been shown that, applying the graphical method to this problem, the optimal solution is the following:
Result
By performing the various methods described above, they all lead to the solution. The solution will be that the optimal value of the objective function is:
Conclusions
Linear programming teaches quantitative decisions about how to use limited resources to maximize a goal, which can be profit or efficiency, while respecting constraints.
Question
Have you ever heard of linear programming? Have you ever done any linear programming exercises in school?

[ITALIAN]
04-11-2025 - Esercizio - Descrizione di un esercizio di Programmazione Lineare [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto svolgendo degli esercizi.
Il contesto in cui operiamo è quello della Ricerca Operativa
(codice lezione/articolo: MS_14)
Programmazione lineare
La programmazione lineare è una materia di studio importante per il settore dell'industria e del trasporto. Essa fa parte di un argomento ancora più ampio che è la Ricerca Operativa.
Esercizio
Prendiamo in considerazione il seguente problema di programmazione lineare, il quale è un problema di minimizzazione
e questo problema è soggetto ai seguenti vincoli
Trasformazione in forma standard
La prima cosa che dobbiamo fare per proseguire con l'esercizio dobbiamo convertirlo in quella che viene chiamata come forma standard.
Per eseguire questa operazione dobbiamo introdurre le variabili di slack .
L'introduzione delle variabili di slack ci servono per trasformare le disequazioni in uguaglianze.
Qui di seguito sono riportati i vincoli trasformati in forma standard con le variabili di slack (colore viola).
Vincoli e variabili
Nella forma standard ora il problema presenta 2 vincoli e 4 variabili.
I vari modi per lo svolgimento del problema
Per risolvere un problema di programmazione lineare possiamo usare il metodo del simplesso. Il Metodo del Simplesso procede generando una sequenza di soluzioni di base ammissibili con valore della funzione obiettivo non crescente, fino a trovare la soluzione ottima o concludere che il problema è illimitato
Per quanto riguarda il problema sopra descritto possiamo definire la matrice dei coefficienti (A), il vettore dei termini noti (b) e i coefficienti della funzione obiettivo (c) .
Per risolvere questo problema possiamo usare anche il metodo del simplesso (fase 2). L'obiettivo del Simplesso (Fase 2) è partire da una soluzione di base ammissibile e iterare attraverso le operazioni di pivot, scambiando colonne in base e fuori base, finché non si soddisfano i criteri di ottimalità.
Si può anche usare il metodo grafico in cui si costruisce il poliedro delle soluzioni e l'ottimo risulterà su uno dei vertici del poliedro.
Ad esempio, è stato dimostrato che, applicando il metodo grafico a questo problema, la soluzione ottima è la seguente:
Risultato
Eseguendo i vari metodi descritti sopra, tutti porteranno alla soluzione. La soluzione sarà che il valore ottimo della funzione obiettivo è:
Conclusioni
La Programmazione lineare insegna a decidere quantitativamente come usare risorse limitate per massimizzare un obiettivo, che può essere di profitto o efficienza, rispettando dei vincoli.
Domanda
Avete mai sentito parlare di programmazione lineare? Avete mai fatto a scuola qualche esercizio di programmazione lineare?
THE END