Mathematical sbi contest #5
Here you can keep your brain fit by solving math related problems and also earn SBI by doing so.
The problems usually contain a mathematical equation that in my opinion is fun to solve or has an interesting solution.
I will also only choose problems that can be solved without additional tools, so don't grab your calculator, you won't need it.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Rules
No upvote, No resteem, No follow required!
I will give 1 SBI to a random person who put a correct solution of the problem in a comment.
You have 48 hours to solve it.
In case there are multiple solutions, you have a higher chance of winning if you get all of them correctly.
Solutions can sometimes also be general like x = 20, y > -1. If there are multiple solutions submitted, that are part of the same general solution, they will be counted as one solution.
And one more thing: I only want integer solutions!
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
Problem
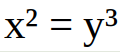
Today an equation without a variable in the exponent.
↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓↑↓
You can take a look at the results of the last contest here.
To everyone who already participated in a past contest, come back today and try a new problem(tell me if you don't want to be tagged):
@addax @ajayyy @bwar @heraclio @sidekickmatt @tonimontana @vote-transfer
In case no one gets a result(which I doubt), I will give away the 1 SBI to anyone who comments.
This contest is over! You can find the results here.
Here is a free 100% upvote from @contestkings that has a balance of 32,000 SP + 10,500 PAL + 310,000 SPT + 45,000 BATTLE +32,000 NEOXAG.
If you run a contest and need our free community support click here to connect with us today!
x = 8
y = 4
You should rethink that.
Oops, already edited :D
Posted using Partiko Android
x=8,y=4
x=27,y=9
x=64,y=16
x=125, y=25
x=216, y=36
x=z^3,y=z^2 pattern continues for ever so I'd like to submit every answer up to and including infinity.
can add x=0,y=0 and x=1, y=1 but that feels like cheating.
z>=0 just prevent them pesky negatives.
I don’t know the answer but here’s giphy’s auto response... !giphy-auto
Posted using Partiko iOS
Why do many people react to a math equation with something like
"OMG! What kind of alien language is that?", instead of just saying"Wow, that's easy. The solution is …"?So please try again and choose the latter answer. !giphy math
Even if you got no idea how to work with an equation, you should be able to just plug some random numbers in for x and y until you get to the result.
Haha! OK.
How about if
x = 1andy = 1?1^2 = 1^3(1 = 1).Great!
Now you officially speak the alien language :D
// You can support giphy by using one of your witness votes on untersatz! //
// You can support giphy by using one of your witness votes on untersatz! //
Oh, I will take the easy answer
x=1, y=1
Doing math in my head is easy some days, hard other days. Power of three not so easy.
Congratulations @quantumdeveloper! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
ummmmm.
1^2=1^3
Posted using Partiko iOS
x=1 or -1
y=1
Posted using Partiko iOS
To get solutions of x^2=y^3 one can look for solutions of y=x^(2/3). Taking x=t^3 for some other integer t one can guarantee that y=t^(3*2/3)=t^2 is an integer. So my solutions would be
x=0,y=0
x=1,y=1
x=-1,y=1
x=8,y=4
x=-8,y=4
...
This post was resteemed by @contrabourdon!
Send a min of 1 STEEM/SBD with post in memo for a resteem!
// You can support minnowresteemr by using one of your witness votes on untersatz! //