Las matemáticas van al cine

¿Tienes tus palomitas? ¿Elegiste tu asiento? ¿Estás cómodo? Entonces dejemos que rueden los créditos.

Todos nos hemos maravillado con las imágenes increíblemente reales simuladas por computadoras en las películas. Lo que la mayoría de nosotros no sabe es que los animales de El Libro de la Selva y la mayor parte de las películas de superhéroes, no sería posible sin las matemáticas.

Pero ¿Cómo se hacen esas maravillosas imágenes? Los gráficos y la visión por computadora son temas amplios. Pero una parte esencial de las matemáticas que quizás veas hacia el final de la secundaria, es la clave para hacer que esta magia pase.

El primer paso para crear una película generada por computadora, es crear a los personajes de la historia y el mundo en el que viven. Cada uno de esos objetos es creado como una superficie hecha de polígonos conectados (generalmente triángulos). Las esquinas de cada triángulo son almacenadas como un espacio tridimensional en la memoria de la computadora. Entonces, esa superficie es sombreada para imitar la luz real usando otro método matemático llamado Trazado de Rayo.

Todo lo que se necesita es un poco de imaginación

Una vez que tu escena esté montada e iluminada, aún esperamos que el director grite “¡Acción!” para que nuestros personajes comiencen a moverse. Y aquí es donde la matemática trae la imagen a la vida.

Una de las maneras más básicas que un objeto se puede mover, es rotando alrededor de un axis dado y a través de un ángulo dado. Estos movimientos de hacen simples usando números complejos esos que involucran el número , donde
.

En particular, necesitamos la interpretación geométrica de los números complejos donde están asociados con puntos en plano bidimensional, con el número real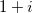 
situado en uno de los axis y el número imaginario situado en el otro. Por ejemplo el número 1 + corresponde al punto (1,1). Generalmente un número complejo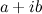
corresponde al punto (a, b).

Veamos qué pasa si multiplicamos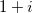
representado en el punto (1,1) por :

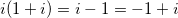
El cual está representado por el punto (-1, 1). Pero el punto (-1, 1) es lo que obtienes cuando giras 90° el punto (1, 1) alrededor del punto (0, 0). Multiplicar por
de nuevo da:

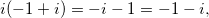
Que es el punto (1, 1), rotado 90° otra vez. Multiplicar por es una instrucción para girar 90°, de hecho, cualquier rotación, no solo la de 90° se puede lograr multiplicando cualquier número complejo.

Moviéndose en 3D

Los marcos de alambres de nuestros personajes, sin embargo, son almacenados como una colección de puntos en el espacio tridimensional. La persona que inventó una forma para rotar las cosas en tres dimensiones es el matemático Sir William Rowan Hamilton, quizás el hijo más famoso de la Universidad de Trinity en Dublin. Él dedicó las últimas dos décadas de su vida buscando la forma de representar las rotaciones tridimensionales de manera similar a como los números complejos pueden representarlas en 2 dimensiones.

El destello de brillantez de Hamilton mientras caminaba bajo el puente Broome en Dublín se llamó cuaterniones. Resulta que los cuaterniones son la más eficiente forma de rotar en tres dimensiones. Pero no todo el mundo estaba contento con su nuevo método de multiplicación. Lord Kelvin, el físico, dijo respecto a los cuaterniones: “Aunque maravillosamente ingeniosos, han sido un mal sin mezcla para aquellos que los han tocado de alguna manera”.

Si alguna vez te has quedado en el cine después de que se acaba la película para mirar como ruedan todos los créditos, está atento a la gran cantidad de talento creativo involucrados en hacer una película exitosa; escritores, directores, actores, diseñadores de vestuario, utileros… la lista es larga. Pero una palabra es usualmente omitida de la lista de créditos, matemáticos.

Muchas de las películas de hoy en día no serían posibles sin la geometría del trazado de rayo o los cuaterniones que hacen girar objetos en el espacio. Así que la próxima vez que te acomodes en el asiento de una sala de cine a disfrutar de una película animada por computadora, levanta tus palomitas por las matemáticas, la estrella oculta del show.

---

Posted from my blog with SteemPress : https://matematicapositiva.com.ve/las-matematicas-van-al-cine/

---