ANÁLISIS INSUMO-PRODUCTO [MODELO DE Wassily Leontief ] / Una aplicación de las matrices a la economía
La interacción entre las industrias de la producción genera interés en los estudios sobre la economía, en especial en los modelos que relacionan la producción y el consumo en términos predictivos. Tal es el caso de Wassily Leontief (1906-1999), economista norteamericano de origen ruso, quien a finales de los 40 propuso un modelo que permitiría realizar un análisis insumo-producto en términos predictivos, ya que predecir los niveles de producción futuros de una industria con el objetivo de satisfacer la demanda futura para diversos productos es el objetivo primordial del modelo de Leontief.

A través del siguiente ejemplo explicaré el modelo.
Supongamos que existen dos empresas productoras P y Q que se interrelacionan ya que para la producción anual de sus productos cada una de ellas necesita insumos que los consigue en la otra.
Tal relación se muestra en el siguiente cuadro:
| Insumos de la empresa P | Insumos de la empresa Q | Producción total | ||
|---|---|---|---|---|
| Producción de la empresa P | 20 | 56 | 100 | |
| Producción de la empresa Q | 50 | 8 | 80 |
Interpretando el cuadro deducimos que la empresa P para su producción anual de 100 unidades de su producto necesita 20 insumos propios y 56 de la empresa Q. Similarmente, la empresa Q necesita 50 insumos de la empresa P y 8 insumos propios para su producción anual de 80 unidades de su producto.
Pero en la producción intervienen otros tipos de insumos, estos insumos tienen que ver con la mano de obra, materias primas, ....; tales insumos los vamos a llamar insumos primarios y los vamos a agregar al cuadro anterior; así como también, los insumos totales de cada empresa.
| Insumos de la empresa P | Insumos de la empresa Q | Producción total | ||
|---|---|---|---|---|
| Producción de la empresa P | 20 | 56 | 100 | |
| Producción de la empresa Q | 50 | 8 | 80 | |
| Insumos primarios | 30 | 16 | ||
| Insumos totales | 100 | 80 |
Observe que el total de los insumos es igual al total de lo que produce cada empresa, esto es válido en un modelo económico donde todo lo que se produce se consume.
En la primera fila del cuadro observamos que la empresa P utiliza 20 insumos propios más 56 de la empresa Q, para un total de 76 insumos para producir 100 unidades, pero el total de insumos debe ser igual a la producción, por lo tanto deja 24 insumos disponibles para la demanda final; esto es, los bienes que no utilizan internamente las empresa productoras y que quedan libres para la demanda externa. En el caso de Q, la demanda final es de 22.
Agreguemos esa categoría al cuadro anterior.
| Insumos de la empresa P | Insumos de la empresa Q | Demandas finales | Producción total | |
|---|---|---|---|---|
| Producción de la empresa P | 20 | 56 | 24 | 100 |
| Producción de la empresa Q | 50 | 8 | 22 | 80 |
| Insumos primarios | 30 | 16 | ||
| Insumos totales | 100 | 80 |
Supongamos que se hace una investigación de mercado que predice que en 5 años, la demanda para P cambia a 74, y para Q la demanda cambia a 37 unidades. Nos preguntamos, ¿a qué tanto cada empresa debería ajustar su nivel de producción a fin de satisfacer esa demanda final proyectada.
Sabemos que la producción de cada empresa está ligada a la otra, y que en 5 años P deberá producir x1 unidades y Q por su lado, deberá producir x2 para satisfacer la demanda proyectada.
De acuerdo a la tabla anterior, la empresa P con la finalidad de producir 100 unidades de su producto utiliza 20 insumos propios, entonces para producir x1 unidades requerirá de 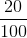 x1 =0.2x1, y
x1 =0.2x1, y 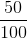 x1=0.5x1 de la empresa Q. Similarmente la empresa Q necesitará para producir la demanda proyectada x2 ,
x1=0.5x1 de la empresa Q. Similarmente la empresa Q necesitará para producir la demanda proyectada x2 , 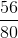 x2=0.7x2 de los insumos de la empresa P, y
x2=0.7x2 de los insumos de la empresa P, y 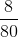 x2=0.1x2 de sus propios insumos.
x2=0.1x2 de sus propios insumos.
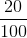 x1 =0.2x1, y
x1 =0.2x1, y 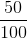 x1=0.5x1 de la empresa Q. Similarmente la empresa Q necesitará para producir la demanda proyectada x2 ,
x1=0.5x1 de la empresa Q. Similarmente la empresa Q necesitará para producir la demanda proyectada x2 , 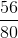 x2=0.7x2 de los insumos de la empresa P, y
x2=0.7x2 de los insumos de la empresa P, y 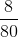 x2=0.1x2 de sus propios insumos.
x2=0.1x2 de sus propios insumos.La producción total de la empresa P deberá ser el resultado de la sumatoria de la unidades consumidas por P más las unidades consumidas por Q más la demanda final dentro de 5 años; esto es:
x1=0.2x1 + 0.7x2 + 74.
De manera similar, de x2 unidades producidas por la industria Q, 0.5x2 los utiliza de P y 0.1x2 las utiliza de Q misma. Esto es: x2= 0.5x2 + 0.1x2 +37 (recuerde que 37 es la demanda proyectada para Q).
De manera similar, de x2 unidades producidas por la industria Q, 0.5x2 los utiliza de P y 0.1x2 las utiliza de Q misma. Esto es: x2= 0.5x2 + 0.1x2 +37 (recuerde que 37 es la demanda proyectada para Q).
Usando matrices las ecuaciones anteriores se pueden escribir así:
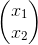 =
= 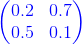
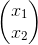 +
+ 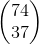
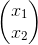 =
= 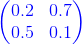
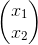 +
+ 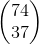
En donde:
X=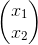 , A=
, A=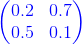 y D=
y D=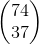
La ecuación X= A X + D recibe el nombre de ecuación "insumo producto". Con la finalidad de conseguir la matriz de producción X que cumplirá con las demandas finales proyectadas. Despejemos X de la ecuación "insumo producto":X - AX= D
Esto es igual a:
(I -A)X=D
Supongamos que (I - A) sea invertible, entonces existe (I-A)-1 tal que:
(I-A)-1(I -A)X=(I-A)-1D
Esto es:
X=(I-A)-1D
Procedimiento que determinará el valor de la matriz producción X.
Para ello debe calcularse:
I-A= 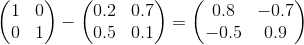
Luego:
( I-A)-1=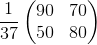
Corresponde resolver ahora:
X= (I-A)-1D=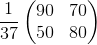
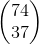 =
= 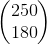
Luego:
X=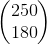
Finalmente, este resultado nos indica que la empresa P deberá producir 250 unidades de su producto, y Q deberá producir 180 unidades para satisfacer las demandas finales proyectadas para dentro de 5 años.
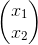 , A=
, A=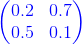 y D=
y D=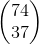
Siendo X la matriz de producción, D es la matriz demanda y A es la matriz insumo-producto, cuyos elementos se denominan coeficientes insumo-producto. Estos elementos están entre 0 y1, y la suma de los elementos de cualquier columna nunca es mayor que 1.
La ecuación X= A X + D recibe el nombre de ecuación "insumo producto". Con la finalidad de conseguir la matriz de producción X que cumplirá con las demandas finales proyectadas. Despejemos X de la ecuación "insumo producto":
Para ello debe calcularse:
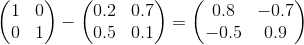
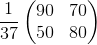
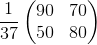
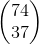 =
= 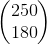
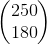
Finalmente, este resultado nos indica que la empresa P deberá producir 250 unidades de su producto, y Q deberá producir 180 unidades para satisfacer las demandas finales proyectadas para dentro de 5 años.
Referencia:
Jagdish C. Arya/Robin W, Lardner.(1989). Matemáticas aplicadas a la administración y a la economía. Prentice Hall Hispanoamericana, S.A.
La imagen de entrada fue hecha con la ayuda de PowerPoint.
Las matrices fueron hechas con la ayuda del editor en línea de ecuaciones LateX:
https://www.codecogs.com/latex/eqneditor.php?lang=es-es

Muy útil su post, @analealsuarez. ¡Siga en esa línea!
Gracias @alexandermoreno, esa es mi finalidad. Saludos.
Oye @AnaLealSuarz, interesante el post. Espero escribir una aplicación que siga principios como los expuestos aquí. Saludos.
Saludos @eniolw, me gustaría ver esa aplicación que piensas hacer. Gracias-