Le modèle de Black-Scholes, en toute simplicité
Avant propos
Cet article a pour but de démontrer "avec les mains" le modèle qui est certainement le plus connu et également le plus utilisé quand on parle de finance de marché, à savoir le fameux modèle de Black-Scholes pour le pricing d'options.
Ici, tout sera expliqué d'une façon qui se veut simple et didactique de façon à bien cerner l'essence du modèle et ce sur quoi il repose.
Cet article est tiré du site web personnel de l'auteur : [http://welcometomyworld.fr/]
Le lemme d'Itô
Comme pour le modèle de Cox-Ross-Rubinstein, nous allons tout d'abord chercher à représenter mathématiquement les fluctuations du prix d'une action au cours du temps.
Par contre, cette fois-ci, le prix de l'action va varier en continue et de manière aléatoire. Nous allons ainsi montrer que l'on peut rendre compte de ce phénomène, à condition de posséder les outils adéquat. Et c'est justement l'objet de cette partie.
Avant toute chose, il est nécessaire d'introduire un concept mathématique abstrait dont nous aurons besoin par la suite dans nos calculs.
Nous parlons ici de phénomènes aléatoires au cours du temps, c'est ce que nous appelons un processus stochastique.
Ainsi, plus académiquement parlant, nous appelerons processus stochastique, une famille de variables aléatoires Xt définies sur le même espace de probabilité.
Pour un certain évenement ω appartenant à l'espace des évènements Ω, la valeur de la varibale aléatoire est : Xt(ω).
Enfin, la trajectoire, encore appelée ensemble des réalisations du processus stochastique est définie par l'application suivante :
Nous définissons alors le processus suivant, appelé processus d'Itô pour la variable aléatoire Xt :
Le lemme d'Itô nous permet alors de définir une différentielle du second ordre pour un processus stochastique :
Le mouvement brownien géométrique
La question est : comment allons-nous pouvoir représenter le prix d'un actif financier au cours du temps, en sachant que celui-ci varie continuellement et de manière aléatoire!
Et bien, pour ce faire, le modèle de Black-Scholes est fondé sur cette hypothèse : le prix d'une action est représenté en tout temps par un mouvement Brownien géométrique. Derrière ce nom, il est vrai quelque peu barbare, se cache la représentation d'un marche totalement aléatoire au cours du temps et qui ne possède pas de mémoire.
Décrit pour la première fois en 1827 par son créateur, le botaniste Robert Brown, qui observait le mouvement de particules à l'intérieur de grains de pollen de Clarkia Pulchella (une fleur sauvage nord américaine), le mouvement Brownien, encore appelé processus de Wiener, décrit la trajectoire aléatoire d'une grosse particule immergée dans un fluide et qui n'est soumise à rien d'autre que des chocs avec les petites molécule du fluide environnant. Depuis lors, ce modèle est extrêmemnt utilisé pour représenter des phénomènes stochastique (variant aléatoirement dans le temps).
Ainsi, par analogie, le prix de l'actif financier va continuer à fluctuer, à la hausse, comme à la baisse; ces fluctuations pouvant être assimilées avec des "chocs", des "intéractions" avec les autres actifs du marché et ceci indépendemment de valeurs précédentes de l'action.
Le prix d'un actif financier se modélise donc par un mouvement Brownien particulier, appelé mouvement Brownien géométrique, qui se présente sous la forme suivante :
Nous pouvons ainsi voir qu'il est composé d'un premier terme totalement prédictif, où μ désigne ce que l'on nomme le drift ou encore la dérive par rapport au temps du prix de l'actif, mais également d'un terme stochastique, comprenez par là totalement aléatoire.
Ce second terme est composé de la volatilité σ et du facteur dB(t), le fameux mouvement Brownien. Ce dernier terme est donc responsable du caractère aléatoire de la valeur de l'actif au cours du temps.
Il est à noter, et c'est une remarque très importante, que les termes μ et σ sont constants dans ce modèle, ce qui va en effet permettre de donner une solution analytique au prix de l'action S(t) en fonction du temps.
En nous servant du lemme d'Itô, nous pouvons obtenir une expresion analytique des fluctuations du prix de l'action au cours du temps.
Il est ainsi possible de transformer l'équation précédente en divisant celle-ci par le terme S(t), supposé bien évidemment non nul :
Nous allons à présent chercher à exprimer cette différentielle plus finement à l'aide d'un développement limité à l'ordre deux.
Nous obtenons ainsi, grâce au lemme d'Itô :
Enfin, il suffit de prendre l'exponentielle de l'expression précédente pour obtenir une formule analytique représentant le prix de l'action en fonction du temps S(t) :
L'équation de Black-Scholes
On part de notre cher lemme d'Itô:
On injecte l'expression décrivant le prix de l'action dans cette expression :
A présent, nous allons regrouper les termes totalement déterministes, facteurs de dt, et isoler le seul terme aléatoire, c'est-à-dire celui contenant le mouvement Brownien dB(t) :
Souvenons-nous de notre portefeuille riskless. Celui-ci est composé d'un nombre constant d'actions, que nous nommerons Δ, et que des options. Fabriquons donc notre portefeuille riskless à partir de l'expression précédente en lui ajoutant nos Δ actions :
Avec l'expression de dS et en réarrangeant un peu de façon à, comme précédemment, séparer les termes déterministes et stochastiques, nous obtenons :
Maintenant, attention les yeux! Nous allons éliminer le risque dans ce portefeuille! Comment faire ? Rien de plus simple : éliminons le terme aléatoire de l'équation!
Des termes s'annulent et nous avons alors :
Or, par définition, avec le taux d'intérêt r :
On réarrange un peu tout ça et on obtient une magnifique équation différentielle stochastique qui n'est autre que la fameuse équation de Black-Scholes :
Le modèle de Black-Scholes
Le modèle de Black-Scholes, ou encore Black-Scholes-Merton, est le modèle le plus utilisé au monde quand on parle d'évaluation d'option. C'est un standard que chaque opérateur de marché connait sur le bout des doigts.
Publié pour la première fois par ses auteurs Fischer Black et Myron Scholes en 1973, celui-ci a connu un succès retentissant et s'est très vite imposé comme le graal des modèles de pricing d'option.
Un peu plus tard, Robert Merton contribuera à l'amélioration de ce modèle ce qui lui vaudra de recevoir, en compagnie de son collègue Myron Scholes, le prix Nobel d'économie en 1997 (Fischer Black étant décédé en 1995, il n'a pu recevoir le prix Nobel, mais sa contibution fut mentionné).
Ultra usité et très réaliste dans une certaine mesure, ce modèle repose cependant sur des hypothèses fortes.
Si cet article vous a plus, n'hésitez pas à laisser un commentaire pour en avoir d'autres du même genre.
An English translation can easily be made if needed.
N'hésitez pas à aller voir le site de l'auteur de l'article également : [http://welcometomyworld.fr/]
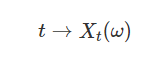
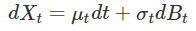
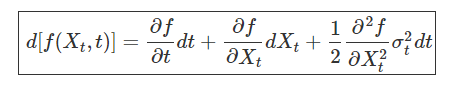
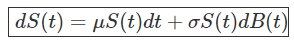
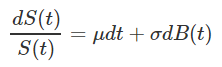
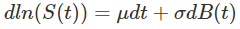
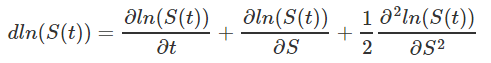
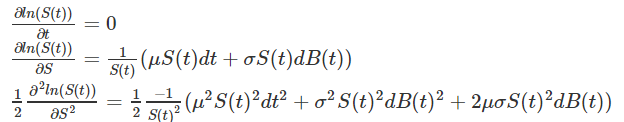
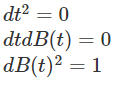
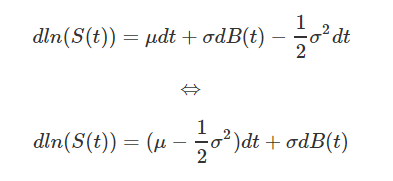
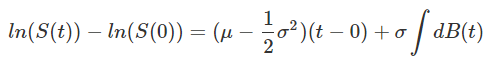
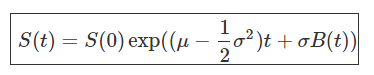
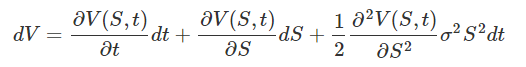
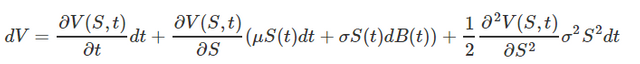
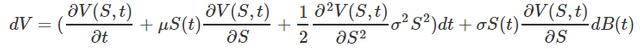
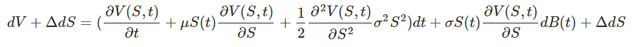
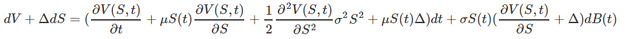
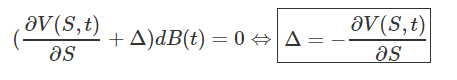
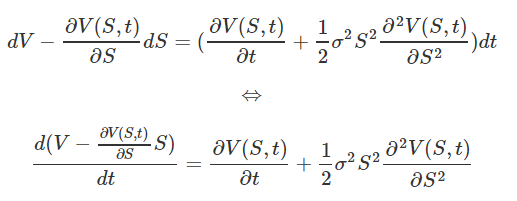
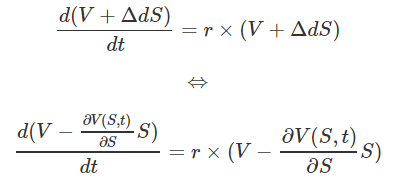
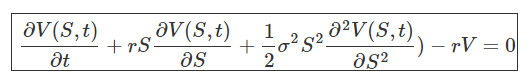

✅ @gentlelife, I gave you an upvote on your first post! Please give me a follow and I will give you a follow in return!
Please also take a moment to read this post regarding bad behavior on Steemit.
Congratulations @gentlelife! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOP