SLC-S22W3//Equations and Systems of equations.

mojociocio (66)in #algebra-s22w3 • 10 months ago

_{Photo taken from Pixabay}

Hello everyone. Today I will take part in week 3 of Steem Learning Challenge, by @khursheedanwar. This week is focused on equations and systems of equations, you can find the original post here.

So, let's get started.

Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms.

We know from the previous week that an equation can be described as a mathematical statement that declares the equality of two expressions, with one or more variables and constants and the use of the equal sign "=" between the expressions.

Now, a system of equations consists of multiple equations (typically two or more) that share variables. The goal is to find values for the variables that satisfy all the equations simultaneously.

Linear Systems of Equations

This type is described as linear because every variable can only be raised to a power of 1 and does NOT include trigonometric or exponential functions
The general form can be written as: a₁x₁ + a₂x₂ + ... + a_nx_n = b. Where:

a₁,a₂,...,a_n are coefficients
x₁,x₂,...,x_n are variables
b is the constant
The graph representation of a linear system is a straight line, a plane or hyperplane
The solution is a single point, a line or no solution

Example:

2x +3y = 8
x - 4y = -5

Non-Linear Systems of Equations

A system of equations is non-linear when there is at least one variable that has a bigger power than 1 or includes trigonometric or exponential functions

The general form can be written as:
f₁(x₁,x₂,...,x_n) = 0,
f₂(x₁,x₂,...,x_n) = 0, ...
Where: f₁, f₂, ... are non-linear functions

The graph representation of a non-linear system can be circles, curves or other shapes
The solutions represent points where all the graphs intersect, resulting in no solution, one or multiple solutions

Example:

x^2 + y^2 = 25
y = 2x^2

Key Differences:

Type	Linear System	Non-linear System
Highest power	1	2
General form	variables appear to first power	variables may appear in power, products etc
Graph Representation	straight line, plane or hyperplane	circles, curves, parabolas, other shapes
Number of solutions	one, none, infinitely	none, one, multiple

The method I chose for task 2 is Matrix Method, by using the idea of inverse matrices.

We can use matrices to represent a system of equations like this: AX = B, where:

A is the matrix for coefficients
X is the column matrix for variables
B is the column matrix for constants

To solve for X, we need to first check if A is invertible and multiply both sides by A^-1, which represents the inverse of A, to isolate X and get: X = A^-1 B which will give the solution.

Given a 2x2 matrix A, we can calculate the inverse of A, and also if it's invertible by using the formula:

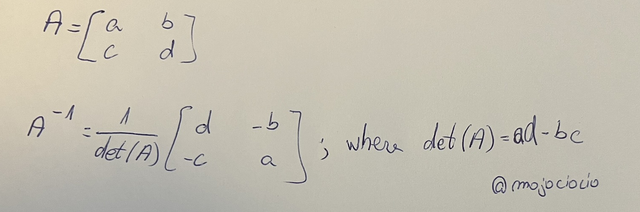
Now, let's take the following example and solve it using the Matrix Method:

2x + 3y = 8
x - 4y = -5

The first step is to write the matrices for A, B and X, and we will have:

A = |2   3|
    |1  -4|

X = |x|
    |y|

B = |8|
    |-5|

And now the system becomes:

|2   3|  |x| = |8 |
|1  -4|  |y|   |-5|

The next step, is to find the determinant of A so we can use it in the formula:

det(A) = (2)(-4) - (1)(3) = -8 - 3 = -11

Using this in the formula for inverse of A, we can write:

 A^-1 = 1/det(A) |-4    -3| = -(1/11) |-4    -3| = |4/11   3/11|
                 |-1     2|           |-1     2|   |1/11  -2/11|

Now that we have the inverse of A, we can finally solve for X by using the formula mentioned above, X = A^-1 B:

X = A^-1 B = |4/11   3/11| * |8|
             |1/11  -2/11|   |5|

We then perform the multiplication like this:

X = |(4/11)(8) +  (3/11)(-5)| = |32/11 - 15/11| = |17/11|
    |(1/11)(8) + (-2/11)(-5)|   |8/11 + 10/11|    |18/11|

By interpreting the X matrix we can write the solution as: x = 17/11 and y = 18/11

The same solve for this can be found in the image below:

In this task, we have to solve 2 systems of linear equation. Let's start with the first one:

x + 2y = 7 (will note it as equation 1)
3x - 2y = 5 (will note it as equation 2)

The solve can be seen in the image below:

EXPLANATION
For this system, I chose the addition method.

By adding the 2 equations together, we can get rid of the y variable and the resulting equation is: 4x = 12
We can solve for x by simply diving the equation by 2 and getting that x = 3.
Now, I will substitute x = 3 in equation 1 and x + 2y = 7 becomes 3 + 2y = 7.
Next step is to move the constant from the left side to the right and have 2y = 7 - 3 => 2y = 4
We solve for y by diving by 2: y = 2

The solution for this system is: x = 3 and y = 2
We can also do a verification of the solution by substituting them in both equations.
Equation 1:

3 + 4 = 7
7 = 7
TRUE

Equation 2:

9 + 4 = 5
5 = 5
TRUE

The second system of equations that we have to solve is:

4x + 6y = 2 (will note it as equation 1)
x - 2y = 3 (will note it as equation 2)

The solve can be found in the image:

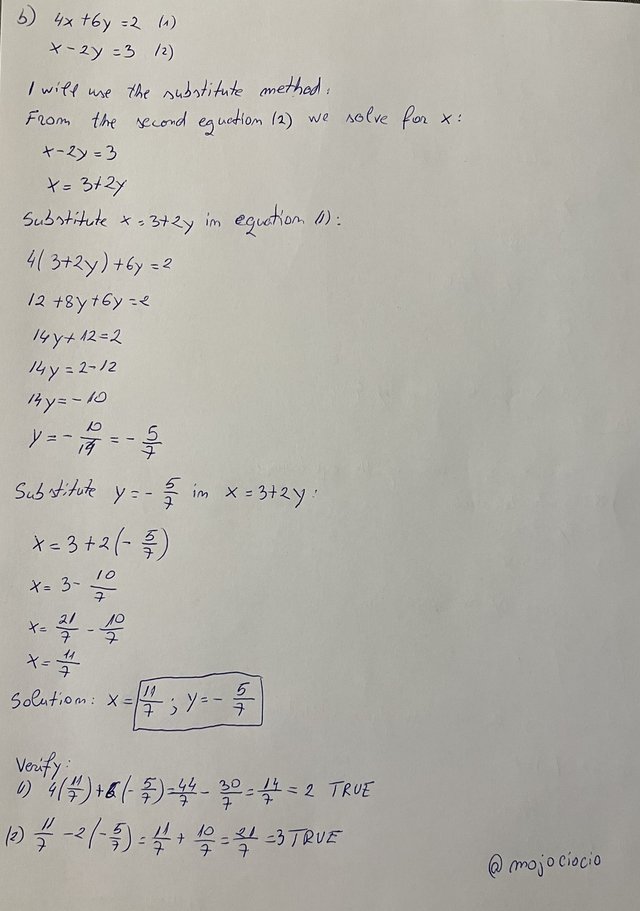
EXPLANATION
For this system, I chose the substitution method.

First, I extracted x from equation 2 and have the expression for x:

x - 2y = 3 => x = 3 + 2y

Next step is to substitute x = 3 + 2y in equation 1 to get this equation: 4(3 + 2y) + 6y = 2
We solve this by first multiplying the parenthesis and get: 12 + 8y + 6y = 2
By adding the coefficients of the variable we have: 12 + 14y = 2
We move the constant on the right side so the variable is alone: 14y = 2 - 12 => 14y = -10
Solve for y and get: y = -(10/14) => y = -(5/7)
Next, we substitute y = -(5/7) in the expression of x: x = 3 + 2[-(5/7)] and get x + 3 - (10/7)
We can write 3 as 21/7 so we have: x = 21/7 - 10/7 => x = 11/7

The solution of the system is: ```x = 11/7 and y = -(5/7)``. Let's verify it:
Equation 1:

44/7 - 30/7 = 2
14/7 = 2
2 = 2
TRUE

Equation 2:

11/7 + 10/7 = 3
21/7 = 3
3 = 3
TRUE

Scenario 1

Suppose there's a company producing two products, A and B.If cost of producing x units of A and y units of B is given by system then; 2x + 3y = 130 (cost of materials); x + 2y = 110 (cost of labor). If company wants for producing 50 units of product A then calculate how much units of product B they may produce?

We are given the system of equation:

2x + 3y = 130 (will note it as equation 1)
x + 2y = 110 (will note it as equation 2)

And that x = 50

With this information, we can substitute x = 50 in equation 1 and solve it:

2(50) + 3y = 130
100 + 3y = 130
3y = 130 - 100
3y = 30
y = 10

From the first equation, we get y = 10.

Also substitute x = 50 in equation 2 to check if we get the same result for y:

50 + 2y = 110
2y = 110 - 50
2y = 60
y = 30

From the first equation, we get y = 30.

We can see that we get conflicted results for y from resolving the 2 equations. From the 1st one we get y = 10 and from the 2nd one we get y = 30. Given this, we can say that the system is INCONSISTENT and there is no solution for it.

Scenario 2

Suppose there's a bakery producing two types of cakes which are vanilla and chocolate. If cost of producing x cakes of vanilla and y cakes of chocolate is given by system then; x + 2y = 80 (cost of ingredients)2x + y = 70 (cost of labor). If bakery wants for producing 30 cakes of vanilla then calculate how much cakes of chocolate can they produce?

We are given the system of equation:

x + 2y = 80 (will note it as equation 1)
2x + y = 70 (will note it as equation 2)

And that x = 30

Again, we start the solve by substituting x = 30 in equation 1 to get a value for y:

30 + 2y = 80
2y = 80 - 30
2y = 50
y = 25

From the first equation, we get y = 25.

Substituting x = 30 in equation 2, we get verify the value for y:

2(30) + y = 70
60 + y = 70
y = 70 - 60
y = 10

From the first equation, we get y = 10.

Resolving the system of equations, we get 2 different values for y when x = 30. This means that the provided system is is INCONSISTENT and there is no solution for it.