Modelado mediante Funciones y Derivadas aplicado a la Teoría Económica, Fundamentos Matemáticos del Análisis Marginal
Saludos a la comunidad de habla hispana y especialmente a la comunidad científica #stem-espanol, en el artículo de hoy estaré abordando una de las aplicaciones de las derivadas de funciones de una variable en la teoría económica, antes de entrar en detalle sobre este tema repasemos algunos conceptos básicos acerca del modelado con funciones.
Imagen N° 1. Fuente: Altmann Gerd (2015), Imagen de Dominio Público CC0. Disponible en Pixabay.
Las matemáticas se usan para describir los fenómenos de la naturaleza y de diversos ámbitos de la actividad humana, en este sentido, el modelado permite abstraer los elementos del mundo real y expresarlos en notación matemática para poder analizar el problema utilizando reglas lógicas y deducciones formales.
En el cálculo diferencial e integral uno de los temas centrales es el análisis de las relaciones entre magnitudes físicas y expresiones matemáticas. Estas relaciones pueden ser descritas en términos de fórmulas, datos numéricos, expresiones o gráficas. Un modelo matemático es una descripción de una ley física en el lenguaje de las matemáticas, cuando una situación ha sido modelada es posible aplicar métodos matemáticos para deducir la solución del problema que se está abordando.
En este orden de ideas, utilizando las leyes de la mecánica de Isaac Newton los científicos pudieron colocar un satélite en órbita alrededor de la tierra, de igual forma, la teoría de la relatividad de Albert Einstein (1879-1955) planteó una serie de leyes que explicaron al detalle el movimiento de la precesión de Mercurio del cual antes solo se tenían hipótesis (incluso una de las hipótesis más inusuales sugería la existencia de un planeta llamado Vulcano en las cercanías del sol que perturbaba la órbita de Mercurio).
El proceso de modelado engloba una serie de fases las cuales parten de la definición clara de la realidad que se desea modelar, luego de esto se expresa esta realidad en lenguaje matemático construyendo el modelo, una vez construido el modelo se procede a resolverlo utilizando las técnicas matemáticas necesarias según sea el caso, finalmente se interpreta la solución para comprender su significado real, esta serie de fases pueden observarse en la imagen N° 2.
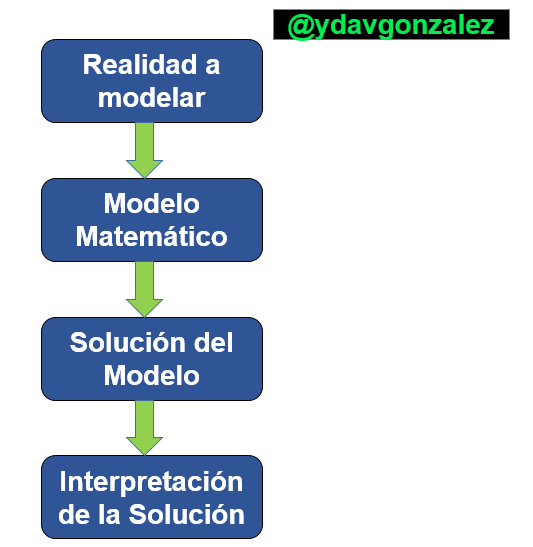
Imagen N° 2 – Esquema sobre el proceso de modelado matemático y resolución de problemas. Fuente: @ydavgonzalez.
Sin embargo, el modelado mediante funciones tiene una amplia gama de aplicaciones que trascienden a la física, un claro ejemplo de esto lo encontramos en la economía la cual se vale de modelos matemáticos para estudiar los fenómenos económicos y de mercado.
Las funciones matemáticas permiten expresar situaciones de la vida cotidiana utilizando el lenguaje matemático, de esta forma facilitan operar con este tipo de expresiones para analizar el comportamiento de los fenómenos estudiados.
La teoría económica es una de las áreas en las cuales las matemáticas tienen especial relevancia al permitir encontrar los niveles de producción que maximizan la ganancia y estudiar las alternativas óptimas en la toma de decisiones.
En el análisis de costos y ganancias el modelado matemático mediante el uso de funciones es de especial interes, uno de los casos más emblemáticos de este aspecto lo representan las funciones referentes a costos, ingresos y ganancias.
La función de costo total de producción C(x) especifica cuánto cuesta producir una cantidad x de producto durante algún período de tiempo.
La función ingreso total de la venta I(x) especifica el ingreso obtenido al vender x cantidad de producto durante algún período de tiempo.
Finalmente la función ganancia G(x) hace referencia a la ganancia total obtenida al producir y vender x cantidad de producto.
Asumiendo que se vendan todas las unidades que se produzcan se cumple que la ganancia es igual al ingreso total menos los costos de producción, es decir
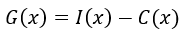
Ahora bien, si se desea determinar la estructura general de esta fórmula se debe tener en cuenta que los ingresos totales de la venta del producto son equivalentes al precio p multiplicado por las unidades de producto vendidas x.
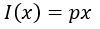
Se puede apreciar que la función ingreso total posee una estructura lineal, en relación a la función de costo de producción su análisis económico se debe centrar en el hecho de que la producción de determinados artículos genera dos tipos de costos, en primer lugar los llamados gastos generales (los cuales incluyen los costos fijos, por ejemplo el alquiler del local y el seguro) estos costos deben pagarse siempre aunque no se produzca ninguna unidad de producto y su valor es constante, por otra parte también están los costos de fabricación M(x) los cuales se refieren a los gastos generados en la fabricación de x unidades de productos tales como el costo de la mano de obra y de los materiales. En base a esto se puede establecer que:
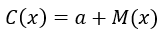
Donde a representa los gastos generales y M(x) los costos de fabricación de x unidades de producto. Por otra parte, en el análisis de las ganancias la expresión que representa los costos de fabricación suele tener la siguiente forma general
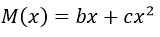
Por lo tanto se cumple que
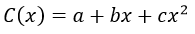
En base a esto, la función de ganancia viene dada por
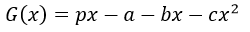
Esta función permite determinar la ganancia de la empresa dependiendo de la cantidad de producto que elabore y venda, se debe tener en cuenta la existencia de restricciones en cuanto al número de empleados, la demanda del mercado, las condiciones económicas, la competencia y la maquinaria disponible, debido a estas condiciones existe algún limite en la producción máxima de la empresa, matemáticamente esto puede expresarse como:
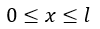
Esto quiere decir que en base a la función de ganancia se debe encontrar el valor de x que maximice el valor de G(x) en el intervalo [0,l] para poder establecer cuantas unidades de producto deben fabricarse para obtener la mayor ganancia posible.
Ejemplo de aplicación:

Imagen N° 3. Fuente: Yanes Diana (2018), Imagen de Dominio Público CC0. Disponible en Pixabay
Una arepera en la ciudad de Coro vende arepas a un precio de Bs. 500.000 por unidad, en relación a los costos de producción por cada arepa gasta Bs. 250.000 entre mano de obra e ingredientes, adicionalmente debe cancelar al gobierno un impuesto cuyo valor porcentual depende del número de arepas que produzca, la tasa de dicho impuesto es de 0,01% por cada arepa que se venda, es decir, en caso de vender 100 arepas la tasa del impuesto del día será igual a 1% del ingreso total, también existen unos costos fijos equivalentes a Bs. 3.000.000, la demanda máxima de arepas en la ciudad es de 4.000, en base a estos datos determine la función de ganancia para el caso de la arepera y el valor óptimo de los niveles de producción.
Se debe recordar la forma general de la función ganancia
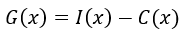
Teniendo en cuenta que el precio es de Bs. 500.000 se cumple que el ingreso total de la venta de las arepas será de:
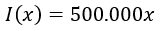
Donde x es la cantidad de arepas vendidas.
En relación a los costos de fabricación, los mismos están compuestos de dos costos, en primer lugar el costo de la mano de obra e ingredientes el cual es igual al costo por unidad multiplicado por x (número de arepas).
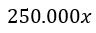
Adicionalmente el impuesto pagado al gobierno, cuya tasa es variable en función del número de arepas vendidas, la tasa de dicho impuesto es de 0,01% por cada arepa que se venda, es decir, su tasa es de:
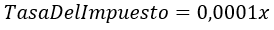
Por lo tanto el valor a pagar es equivalente a la tasa del impuesto multiplicado por los ingresos totales percibidos
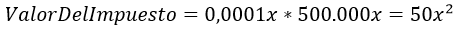
Sumando ambos costos, se obtiene un valor para los costos de fabricación de
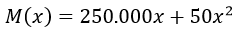
Para determinar la expresión relativa a los costos totales de producción se debe tener en cuenta la existencia de un costo fijo de Bs. 3.000.000, por lo tanto el costo total de producción es
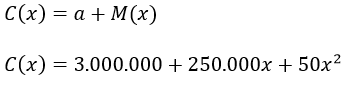
Luego sustituyendo los valores obtenidos en la función ganancia
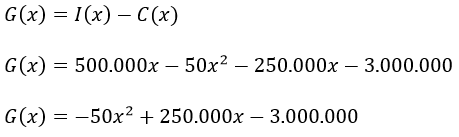
Esta función permite calcular la ganancia obtenida por la venta de x arepas. Como la demanda máxima de arepas es de 4.000 la función G(x) está definida en el intervalo
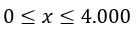
Para determinar el punto óptimo de producción que maximiza la ganancia se debe encontrar el máximo absoluto de la función G(x) en el intervalo en que está definida, el máximo absoluto según Anton, Biven y Davis (2010) se define de la siguiente forma:
Sea I un intervalo en el dominio de una función. Se dice que f tiene un máximo absoluto en el punto x0 de I si f(x) ≤ f(x0) para toda x en I, y se dice que f tiene un mínimo absoluto en x0 si f(x0) ≤ f(x) para toda x en I. Se dice que f tiene un extremo absoluto en x0 si tiene ya sea un máximo absoluto o un mínimo absoluto en ese punto.
Para encontrar los extremos absolutos de una función en un intervalo I se utiliza el siguiente procedimiento:
Paso 1. Se encuentran los puntos críticos de la función en el intervalo (los puntos críticos son aquellos en que la derivada de la función es igual a cero o no esta definida).
Paso 2. Se evalúa la función en todos los puntos críticos y en los puntos finales del intervalo (a,b).
Paso 3. El mayor de los valores obtenidos en el paso 2 es el valor del máximo absoluto de la función en el intervalo [a,b] y el valor menor corresponde al mínimo absoluto.
Aplicando este procedimiento a la función de ganancia planteada anteriormente se obtiene
Paso 1
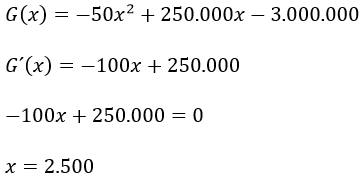
Paso 2
Como la función G(x) está definida en el intervalo
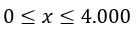
Se debe evaluar G(x) en 0 ; 2.500 y 4.000
Paso 3
Se evalúa la función G(x) en los puntos obtenidos en el paso número 2.
| Arepas Vendidas | 0 | 2.500 | 4.000 |
| Ganancia (Bs.) | -3.000.000 | 309.500.000 | 197.000000 |
Tabla N° 1 Relación entre el número de arepas vendidas y la ganancia obtenida. Fuente:@ydavgonzalez.
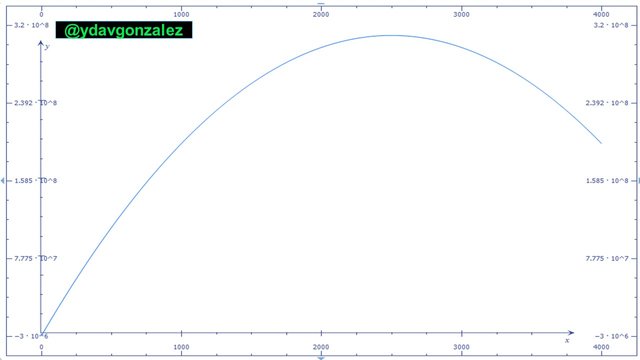
Es decir, el valor que maximiza las ganancias de la arepera es el de 2.500 arepas diarias, lo cual concuerda con la gráfica de la función ganancia.
Imagen N° 4 – Gráfica de la función ganancia total, elaborada mediante el programa Matemáticas de Microsoft y editada por el autor. Fuente: @ydavgonzalez.
En este punto los ingresos, costos y ganancias totales son iguales a
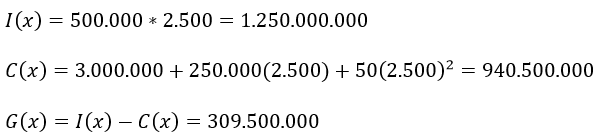
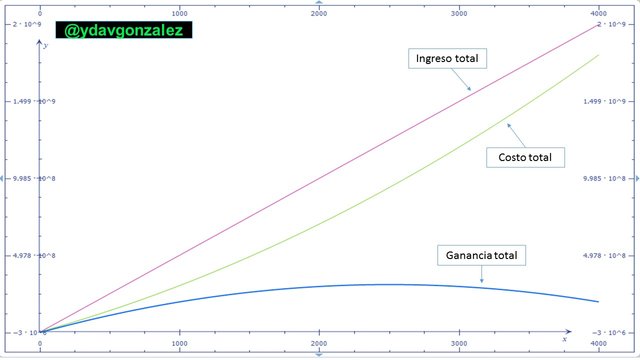
Obteniendo una ganancia total de Bs. 309.500.500 Diarios, el comportamiento la ganancia, ingresos y costos se pueden apreciar en la siguiente imagen.
Imagen N° 5 – Gráfica de las funciones ganancia total, costo total e ingreso total elaborada mediante el programa Matemáticas de Microsoft y editada por el autor. Fuente: @ydavgonzalez.
Hasta aquí se ha utilizado el modelado matemático mediante funciones y derivadas para encontrar el valor que maximiza las ganancia de la arepera, sin embargo, la teoría económica no se limita a solo eso, también analiza este tipo de problemas desde el enfoque marginal el cual permite determinar lo que los economistas denominan ganancia marginal G’(x), ingreso marginal I’(x) y costo marginal C’(x) los cuales corresponde a la ganancia, ingreso y costo adicionales como resultado de producir y vender una unidad más de producto en el momento en que los niveles de producción se encuentran en x unidades.
En el ejemplo anterior se puede determinar la ganancia, costo e ingresos marginales para el valor óptimo de producción y venta de arepas.
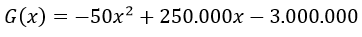
Se calcula la primera deriva para obtener la ganancia marginal
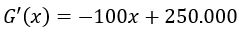
Sus sustituye x por 2.500
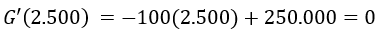
Como se puede observar en el máximo absoluto la ganancia marginal es de cero, lo cual está en concordancia con uno de los principios básicos del análisis marginal que plantea que:
La ganancia máxima ocurre cuando el costo de fabricar y vender una unidad adicional de un producto es aproximadamente igual al ingreso generado por la unidad adicional.
Evidentemente si el ingreso y costo marginal son iguales, entonces la ganancia al ser la resta de estos dos valores será cero. Se puede observar que se cumple dicha igualdad, teniendo en cuenta que el costo marginal es igual a
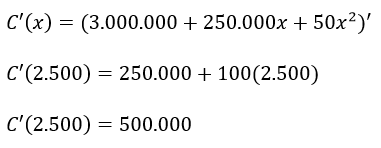
En relación al ingreso marginal
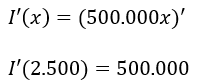
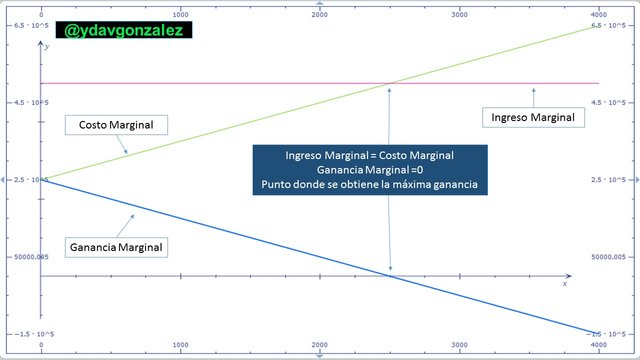
Por lo tanto en el máximo absoluto el ingreso marginal y el costo marginal están igualados. Estos resultados se pueden apreciar de forma gráfica en la siguiente imagen.
Imagen N° 6 – Gráfica del análisis marginal elaborada mediante el programa Matemáticas de Microsoft y editada por el autor. Fuente: @ydavgonzalez.
Se observa que en el punto en que la ganancia marginal cae por debajo de cero deja de ser rentable producir y vender arepas debido a que cada arepa adicional que se elabore y venda producirá perdidas, en este punto también están igualados el ingreso marginal y el costo marginal, por esta razón la ganancia es máxima.
CONCLUSIONES
- El análisis de funciones tiene innumerables aplicaciones más allá de las ciencias básicas, la teoría económica es un terreno fértil para establecer modelos matemáticos utilizando funciones.
- La primera derivada de una función permite obtener los puntos críticos los cuales son usados para determinar los extremos absolutos, lo cual en problemas de aplicación se traduce en encontrar los valores máximos y mínimos.
- El modelado mediante funciones permite utilizar técnicas matemáticas para resolver problemas de diferente índole.
REFERENCIAS BIBLIOGRÁFICAS Y LECTURAS RECOMENDADAS
Anton, Bivens y Davis (2010), Cálculo de una variable, Trascendentes tempranas. 2da edición Editoria Limusa Willey.
Godoy (1981). Teoría Económica I. Universidad Nacional Abierta. Décima Octava reimpresión.
Saenz (2009), Cálculo Integral con Funciones Trascendentes Tempranas para Ciencias e Ingeniería. 2da edición Editorial Hipotenusa.
Sauer (2013), Análisis Numérico. 2da edición Editorial Pearson.
Definitivamente la matemáticas es una ciencia madre con cabida en todos los ámbitos de la vida. Muy bueno el ejemplo de las arepas ja,ja,ja.
Gracias por el apoyo @elvigia, saludos.
Este es el post mas genial de las matematicas que he leido, aunque debo decir que en las graficas soy un ocho, entendi lo esencial. Muy buen post.
Gracias @ricardo993 es cuestión de analizarlas con detenimiento.
Seria interesante un video explicando las gráficas... Sigue dando lo máximo. Felicidades.
¡Este es el mejor que he leído en español últimamente! Este es el espíritu exacto de la escritura innovadora que siempre he estado buscando y estoy feliz de que haya decidido compartirlo con nosotros. No olvide de agregar @originalworks Upvoted & Resteemed. ∜mp
Este post fue compartido en el canal hispano #la-colmena de la comunidad de curación Curation Collective y obtuvo upvote y resteem por la cuenta de la comunidad @c-squared después de su curación manual.
This post was shared in the #la-comena channel in the Curation Collective Discord community for curators, and upvoted and resteemed by the @c-squared community account after manual review.
Hi @ydavgonzalez!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
This post has received a 0.39 % upvote from @drotto thanks to: @ydavgonzalez.
Congratulations @ydavgonzalez! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPBuen diaz! It took me a wille to translate this :)) Nice post!;)