Mathématiques : algèbre linéaire 3 - Existence d'une base dans un espace vectoriel -

(couverture du " Joseph Grifone ")

Nous avons vu ce qu'était une famille libre (et liée) ainsi qu'une famille génératrice dans les deux posts précédents. J'avais pris comme bases de référence, les bases canoniques de R2 ET R3 sans forcément définir la notion de '' base d'un espace vectoriel ''. En effet, ces deux bases sont très intuitives et ne demande pas de connaissances particulières pour être à même de les appréhender. 

L'existence d'une base dans un espace vectoriel est néanmoins plus subtil qu'il n'y paraît. Afin de tuer tout suspense d'entrée de jeu, sachez qu'une famille de vecteurs à la fois libre et génératrice forme automatiquement une base dans un espace vectoriel. Les deux conditions doivent être remplies (une seule n'est pas suffisante) 

Ce qui est intéressant, c'est surtout de comprendre pourquoi et de regarder ce que cela implique. 

Prenons un point de l'espace R3 et définissons O, l'origine de la base canonique. Soit O (0,0,0) et le point A (5,2,7). Dans cette base, on a donc le vecteur OA (5,2,7). Ceci est trivial. La première question à se poser est la suivante : comment le point A peut-il être atteint à partir de la base canonique ? Pour cela, imaginez que vous devez atteindre le point A en marchant dans le réseau de R3, c'est à dire uniquement sur l'axe x,y ou z, dans cet ordre. On se rend compte assez rapidement qu'il n'existe qu'une seule façon de rejoindre A : 5 pas sur x, 2 sur y et 7 sur z.(voir démonstration un peu après) 

Cette notion se généralise en fait à n'importe quelle base de dimension finie. Ainsi, si on prend un vecteur arbitraire d'un espace vectoriel, ce vecteur ne peut être exprimé que de manière unique comme combinaison linéaire des vecteurs de la base en question. Dans notre exemple, nous avons : 

 OA = 5(1,00) + 2(0,1,0) + 7(0,0,1) 

On dit, et cela est très important, qu'il y a unicité de la décomposition. 

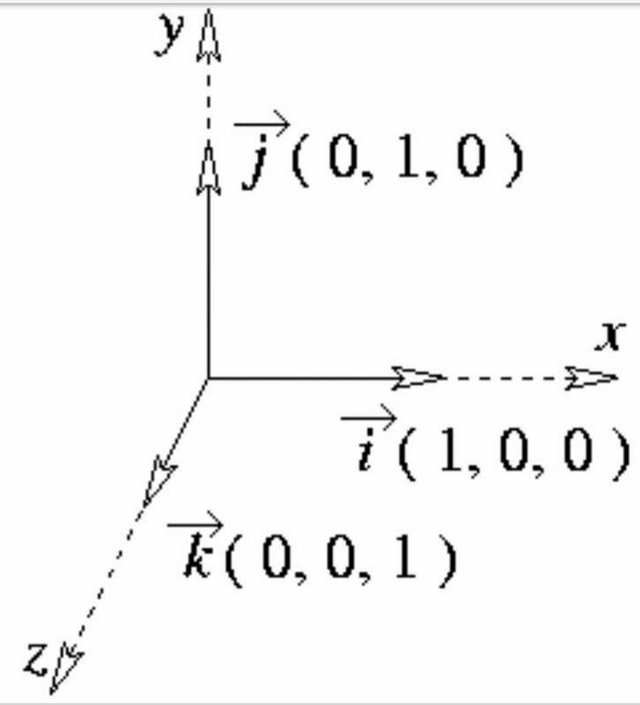
Vecteurs de la base canonique de R3

Soit B un point arbitraire de l'espace. Existe-t-il une façon d'exprimer une combinaison linéaire du vecteur OB ? 

Oui car la famille de vecteurs de notre base est par définition, comme dit plus haut, génératrice. Donc nous pouvons construire n'importe quel vecteur de R3. De plus, cette décomposition sera unique de par la liberté de la famille en question. Pour s'en convaincre, il suffit de supposer deux décompositions différentes d'un vecteur V et de les soustraire. Par exemple : (considérez ce qui suit comme une notation vectorielle pour V,i,j,k)

V = xi + yj + zk
V = x'i + y'j + z'k
V – V = (x-x')i + (y-y')j + (z-z')k = 0 

La famille de la base étant libre par définition, nous avons : 

x-x' = y-y' = z-z' = 0  (voir post sur les familles libres si cela n'est pas clair)

et donc x = x', y = y' et z = z' ce qui termine la preuve et prouve l'unicité de la décomposition. 

Une notion importante liée à la dimension de l'espace vectoriel intervient : dans Rn, la base sera constituée de n vecteurs. Ceci est beaucoup moins évident qu'intuitif ! 

En effet, supposons l'existence de n vecteurs dans R3 formant une famille génératrice, avec n > 3. Cette famille est-elle une base de R3 ? La réponse est non, tout simplement parce qu'il n'est pas possible d'avoir la liberté dans ce cas. La famille considérée ne peut pas être libre car elle sera obligatoirement liée. (essayez de le démontrer, ce n'est pas très difficile) 

De même, supposons une famille libre dans R3 comportant n vecteurs avec cette fois n < 3. Cette famille peut-être une base de R3 ? Là encore ce n'est pas possible. Essayons de le prouver en trouvant un contre-exemple.   

Soient les deux vecteurs de R3 (1,0,0) et (0,1,0). La famille est trivialement libre mais on voit facilement qu'un point avec une coordonnées z non nul ne peut pas être atteint. Ainsi la famille en question n'est pas une base. 

Une famille de vecteurs dans R3, génératrice, doit avoir au maximum 3 vecteurs pour être candidate pour former une base (sinon elle est liée). Une autre famille de vecteurs dans R3, libre, doit par contre avoir au minimum 3 vecteurs pour être candidate (sinon elle ne peut pas être génératrice). Comme on sait qu'une famille de R3 doit être libre et génératrice pour former une base, elle aura donc obligatoirement 3 vecteurs. (seul cas possible) Et cela se généralise dans Rn.(on parle bien des dimensions finies). Ainsi, une base de Rn est composée de n vecteurs.