Explicaciones Matemáticas - Conociendo las Integrales y sus propiedades

steenshare (47)in #stem-espanol • 6 years ago

Hola amigos saludos , tiempo sin saber en que área publicar hasta que pensé porque no publicar sobre lo que me gusta sobre lo que hago , y pues llegue a la conclusión , de realizar una serie de publicaciones sobre la ciencia de las matematicas la cual estará apoyada con ejercicios realizados por mi persona , esta serie la llamaremos , Explicaciones Matematicas , hoy como primera entrega de esta serie hablaremos sobre la integral si esa propiedad matemática que a muchos de nosotros nos dio un gran dolor de cabeza en la universidad , pero que hoy sin duda algunas es una de las propiedades mas importante en esta ciencia , pues bien amigos sepamos que es una integral aquí. En matemáticas, una integral asigna números a las funciones de una manera que puede describir desplazamiento, área, volumen y otros conceptos que surgen al combinar datos infinitesimales. La integración es una de las dos operaciones principales del cálculo, con su operación inversa, diferenciación, siendo el otro. Dada una función f de una variable real xy un intervalo [a, b] de la línea real, la integral definida.

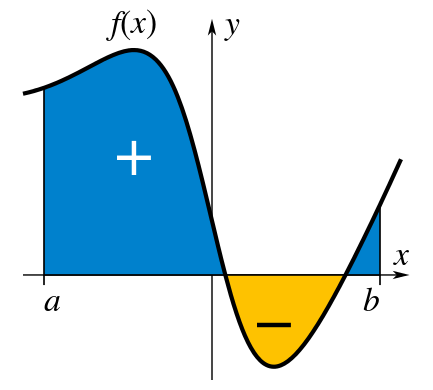
Fuente de la imagen :Una integral definida de una función se puede representar como el área firmada de la región delimitada por su gráfica.Uso de la imagen de Wikipedia

se define informalmente como el área firmada de la región en el plano xy que está delimitada por la gráfica de f, el eje xy las líneas verticales x = a y x = b. El área sobre el eje x se suma al total y la que está debajo del eje x resta del total.

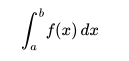
La operación de integración, hasta una constante aditiva, es la inversa de la operación de diferenciación. Por esta razón, el término integral también puede referirse a la noción relacionada de la antiderivada, una función F cuya derivada es la función dada f. En este caso, se llama integral indefinida y está escrito:

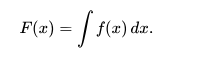
Las integrales discutidas en este artículo son aquellas llamadas integrales definidas. Es el teorema fundamental del cálculo que conecta la diferenciación con la integral definida: si f es una función continua de valores reales definida en un intervalo cerrado [a, b], entonces, una vez que se conoce una antiderivada F de f, la integral definida de f sobre ese intervalo está dado por

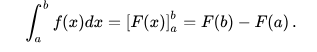
Los principios de integración fueron formulados independientemente por Isaac Newton y Gottfried Wilhelm Leibniz a fines del siglo XVII, quienes pensaban en la integral como una suma infinita de rectángulos de ancho infinitesimal. Bernhard Riemann dio una rigurosa definición matemática de integrales. Se basa en un procedimiento de limitación que se aproxima al área de una región curvilínea al dividir la región en losas verticales delgadas. A partir del siglo XIX, comenzaron a aparecer nociones más sofisticadas de integrales, donde se generalizó el tipo de función y el dominio sobre el que se realiza la integración. Una integral de línea se define para las funciones de dos o más variables, y el intervalo de integración [a, b] se reemplaza por una curva que conecta los dos puntos finales. En una integral de superficie, la curva se reemplaza por una parte de una superficie en el espacio tridimensional.

Aplicaciones

Las integrales se utilizan ampliamente en muchas áreas de las matemáticas, así como en muchas otras áreas que se basan en las matemáticas.

Por ejemplo, en la teoría de la probabilidad, las integrales se usan para determinar la probabilidad de que alguna variable aleatoria caiga dentro de un cierto rango. Además, la integral bajo una función de densidad de probabilidad completa debe ser igual a 1, lo que proporciona una prueba de si una función sin valores negativos podría ser una función de densidad o no.

Las integrales se pueden usar para calcular el área de una región bidimensional que tiene un límite curvo, así como para calcular el volumen de un objeto tridimensional que tiene un límite curvo.

Las integrales también se utilizan en física, en áreas como la cinemática para encontrar cantidades como el desplazamiento, el tiempo y la velocidad. Por ejemplo, en movimiento rectilíneo, el desplazamiento de un objeto sobre el intervalo de tiempo [a, b] está dado por:

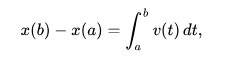
donde v (t) es la velocidad expresada como una función del tiempo. El trabajo realizado por una fuerza F (x) (dada en función de la posición) desde una posición inicial A hasta una posición final B es:

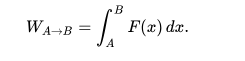
Las integrales también se usan en termodinámica, donde la integración termodinámica se usa para calcular la diferencia en energía libre entre dos estados dados.

Propiedades

Linealidad

La colección de funciones integrables de Riemann en un intervalo cerrado [a, b] forma un espacio vectorial bajo las operaciones de adición y multiplicación puntuales por un escalar, y la operación de integración

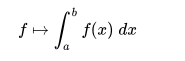
es un funcional lineal en este espacio vectorial. Por lo tanto, en primer lugar, la colección de funciones integrables se cierra bajo combinaciones lineales; y, en segundo lugar, la integral de una combinación lineal es la combinación lineal de las integrales,

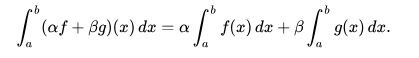
De manera similar, el conjunto de funciones integrables de Lebesgue de valor real en un espacio de medida dado E con una medida μ se cierra al tomar combinaciones lineales y, por lo tanto, formar un espacio vectorial, y la integral de Lebesgue

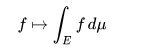
es un funcional lineal en este espacio vectorial, por lo que

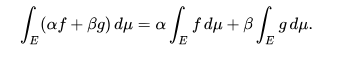
Más generalmente, considere el espacio vectorial de todas las funciones medibles en un espacio de medida (E, μ), tomando valores en un espacio vectorial topológico completo V compacto localmente sobre un campo topológico localmente compacto K, f: E → V. Entonces uno puede definir un mapa de integración abstracto que asigna a cada función un elemento de V o el símbolo ∞,

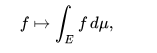
eso es compatible con combinaciones lineales. En esta situación, la linealidad se cumple para el subespacio de funciones cuya integral es un elemento de V (es decir, "finito"). Los casos especiales más importantes surgen cuando K es R, C o una extensión finita del campo Qp de números p-adic, y V es un espacio vectorial de dimensión finita sobre K, y cuando K = C y V es un Hilbert complejo espacio.

La linealidad, junto con algunas propiedades naturales de continuidad y la normalización para una cierta clase de funciones "simples", pueden usarse para dar una definición alternativa de la integral. Este es el enfoque de Daniell para el caso de las funciones de valores reales en un conjunto X, generalizado por Nicolas Bourbaki para funciones con valores en un espacio vectorial topológico localmente compacto. Ver (Hildebrandt 1953) para una caracterización axiomática de la integral.

Teorema fundamental del cálculo

El teorema fundamental del cálculo es la afirmación de que la diferenciación y la integración son operaciones inversas: si una función continua se integra primero y luego se diferencia, se recupera la función original. Una consecuencia importante, a veces llamada el segundo teorema fundamental del cálculo, permite calcular integrales mediante el uso de una antiderivada de la función que se va a integrar.

Declaraciones de teoremas

Teorema fundamental del cálculo

Sea f una función continua de valores reales definida en un intervalo cerrado [a, b]. Sea F la función definida, para todo x en [a, b], por

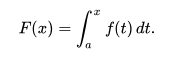
Entonces, F es continuo en [a, b], diferenciable en el intervalo abierto (a, b), y

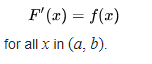
Segundo teorema fundamental del cálculo

Sea f una función de valor real definida en un intervalo cerrado [a, b] que admite una antiderivada F en [a, b]. Es decir, f y F son funciones tales que para todo x en [a, b],

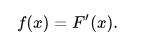
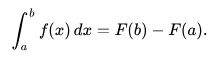
Calculando integrales

El segundo teorema fundamental permite que muchas integrales se calculen explícitamente. Por ejemplo, para calcular la integral

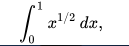
de la función raíz cuadrada f (x) = x1 / 2 entre 0 y 1, es suficiente encontrar una antiderivada, es decir, una función F (x) cuya derivada es igual a f (x):

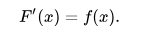
Una de esas funciones es F (x) = 2/3 x3 / 2. Entonces el valor de la integral en cuestión es

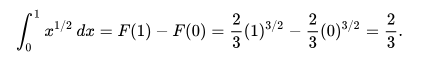
Este es un caso de una regla general, que para f (x) = xq, con q ≠ -1, la función relacionada, la llamada antiderivada es F (x) = xq + 1 / (q + 1). Las tablas de esta y otras antiderivadas similares se pueden usar para calcular integrales de manera explícita, de forma muy similar a como se pueden usar tablas de derivadas.

Integrales de línea

El concepto de integral se puede extender a dominios más generales de integración, como líneas curvas y superficies. Tales integrales se conocen como integrales de línea e integrales de superficie, respectivamente. Estos tienen aplicaciones importantes en física, como cuando se trata de campos de vectores.

Fuente de imagen :Una línea integral suma elementos a lo largo de una curva.Uso de imagen Wikipedia

Una integral de línea (a veces llamada integral de ruta) es una integral donde la función a integrar se evalúa a lo largo de una curva. Varias integrales de línea diferentes están en uso. En el caso de una curva cerrada, también se denomina integral de contorno.

La función a integrar puede ser un campo escalar o un campo vectorial. El valor de la integral de línea es la suma de los valores del campo en todos los puntos de la curva, ponderado por alguna función escalar en la curva (comúnmente la longitud del arco o, para un campo vectorial, el producto escalar del campo vectorial con un diferencial vector en la curva). Esta ponderación distingue la integral de línea de las integrales más simples definidas en intervalos. Muchas fórmulas simples en física tienen análogos continuos naturales en términos de integrales de línea; por ejemplo, el hecho de que el trabajo es igual a la fuerza, F, multiplicado por el desplazamiento, s, puede expresarse (en términos de cantidades de vectores) como:

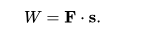
Para un objeto que se mueve a lo largo de una trayectoria C en un campo vectorial F, como un campo eléctrico o campo gravitatorio, el trabajo total realizado por el campo sobre el objeto se obtiene sumando el trabajo diferencial realizado al pasar de s a s + ds. Esto le da a la línea integral

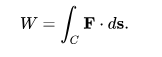
Integrales de superficie

Una integral de superficie es una integral definida tomada sobre una superficie (que puede ser un conjunto curvo en el espacio); se puede considerar como el doble análogo integral de la integral de línea. La función a integrar puede ser un campo escalar o un campo vectorial. El valor de la integral de superficie es la suma del campo en todos los puntos de la superficie. Esto se puede lograr dividiendo la superficie en elementos superficiales, que proporcionan la división de las sumas de Riemann.

Fuente de imagen :La definición de integral de superficie se basa en dividir la superficie en pequeños elementos superficiales.Uso de imagen Wikipedia

Para un ejemplo de aplicaciones de integrales de superficie, considere un campo vectorial v en una superficie S; es decir, para cada punto x en S, v (x) es un vector. Imagine que tenemos un fluido que fluye a través de S, de modo que v (x) determina la velocidad del fluido en x. El flujo se define como la cantidad de fluido que fluye a través de S en la cantidad de tiempo de la unidad. Para encontrar el flujo, necesitamos tomar el producto escalar de v con la superficie de la unidad normal a S en cada punto, lo que nos dará un campo escalar, que integramos sobre la superficie:

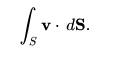
El flujo de fluido en este ejemplo puede ser de un fluido físico tal como agua o aire, o de flujo eléctrico o magnético. Por lo tanto, las integrales de superficie tienen aplicaciones en física, particularmente con la teoría clásica del electromagnetismo.