오일러 공식의 증명 (feat.박사가 사랑한 수식)
[ 박사가 사랑한 수식 (written by 오가와 요코 http://goo.gl/tBMEHy ... 영화도 있었군요!) ] 에 나오는
"아름다움의 극치"인 수식은 아래와 같이 생겼는데,
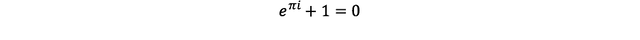
"끝없는 무리수 e의 곁에서
원주율 파이가
상상의 수 i와 손을 잡고
거기에 단 1만 더하면
0이 된다..."
라는 감각적인 설명까지 더해짐으로써,
나에게는 그저 경외의 존재였을 뿐,
그 증명을 이해해보려는 노력 조차 해본 적이 없었다.. (Ignorance is bliss.. 마냥 편했다.)
그러다가 정말 우연히 약 2주 전에
푸리에 변환 (Fourier Transformation)을 너무 쉽게 설명해준 책이라며 추천 받은
[수학으로 배우는 파동의 법칙 https://goo.gl/TtdCDq ]을 슥슥 읽다가..
전혀 예상치 못한 순간에 위 오일러 공식의 증명을 만나서,
감동&감사한 마음에...
그 증명을 여기에 옮기며, 나도 다시한번 그 증명을 마음속에 새겨넣고자 한다.
[ Step 1 ] : 매클로린 전개 (Maclaurin expansion)를 만나자.
그 어떤 함수라도 a0에서 an까지의 계수를 구할 수만 있다면 다음과 같은 형태로 나타낼 수 있다는 것이 매클로린의 개념이다.
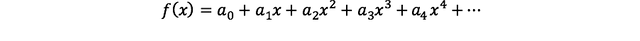
- 그러면, a0부터 구해보자.
좌우변에 x=0을 넣으면
f(0) = a0으로 쉽게 구할 수 있다.
- 그 다음 a1은 어떻게 구할 수 있을까...
위에서 했던 것처럼 x=0을 넣으면 x^2, x^3, ... 이후 뿐만 아니라, a1*x^1까지 사라지는데 어떤 방법이 있을까?
... 아, "미분을 하면 되겠구나...!" (* 이런 직관이 뛰어난 분들을 천재 수학자...라고 부르는 것 같다..........)
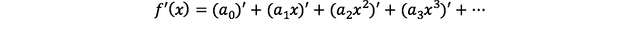
즉, 아래와 같이 정리되고
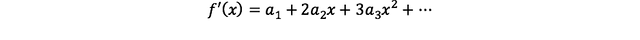
좌우변에 x=0을 넣으면
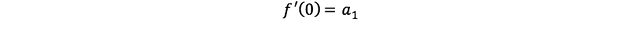
자 a1을 구했다.
뭐든지 초기값 a0와 그 다음 방향성에 해당하는 a1을 찾기만 하면, a2 이후부터는 쉬워지는 법이다.
f'(x)에 미분을 한번 더 해서 f''(x)를 구하면 a2를 구할 수 있을 것이다.
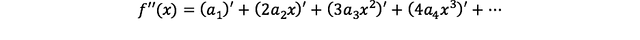
즉,
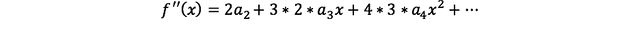
마찬가지로 좌우변에 x=0을 대입하자.
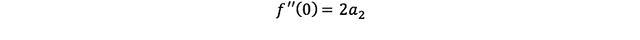
감이 온다.
확실히 느낌을 알기 위해 한번만 더 수고를 해본다면,
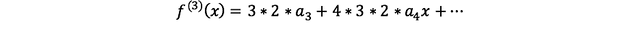
따라서,
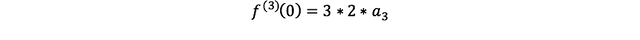
즉,
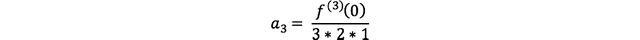
와 같이 정리되고,
아래와 같이 일반화할 수 있겠다...!!
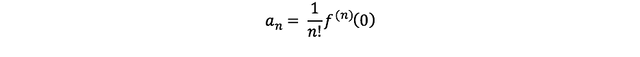
매클로린 전개 공식을 정리하자면,
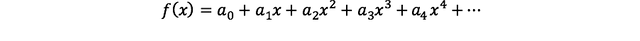
는
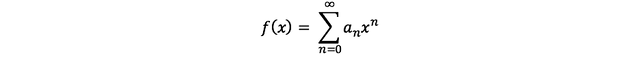
로 다시 표현할 수 있고,
위의 an을 여기에 넣으면,
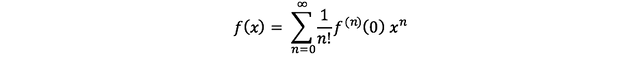
와 같이 정리된다.
이와 같이 매클로린 전개 공식이라는 소중한 무기를 얻게 되었는데,
다시한번 정리하자면,
모든 함수는 위와 같은 무한한 다항식의 형태로 풀어놓을 수 있으며,
미분하여 x=0을 대입하는 스킬을 통해 각 계수 an를 구할 수 있었다.
[ Step 2 ] : Meet the sin(x) and cos(x) w/Maclaurin
추억의 sin(x)와 cos(x)의 미분식은 아래와 같은데...
sin'(x) = cos(x)
cos'(x) = -sin(x)
그렇다면, f(x) = sin(x)로 하고, 미분을 4번 해보면...
f(x) = sin(x)
f'(x) = cos(x)
f''(x) = -sin(x)
f'''(x) = -cos(x)
f''''(x) = sin(x) = f(x)
. f''''(x) = f(x)와 같다는 사실을 알 수 있다. 즉, 4의 주기로 계수가 반복되는 특징이 있을 것임을 알 수 있고,
여기에 각각 0을 대입한다면,
f(0) = 0
f'(0) = 1
f''(0) = 0
f'''(0) = -1
f''''(0) = f(0) = 0
...
0,1,0,-1,...을 반복함을 알 수 있다.
따라서, sin(x)를 매클로린 전개한다면, 다음과 같고
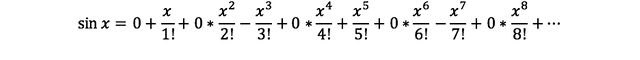
이를 다시 보기 좋게 정리하면
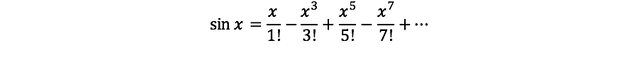
와 같이 정리된다. (#식1)
... 뭔가 약간 신나고 두근거린다. cos(x)에 대해서도 해보자.
f(x) = cos(x)로 놓고, 미분을 4번 해보면,
f(x) = cos(x)
f'(x) = -sin(x)
f''(x) = -cos(x)
f'''(x) = sin(x)
f''''(x) = cos(x) = f(x)
가 되고,
마찬가지로 x=0을 넣는다면
f(0) = 1
f'(0) = 0
f''(0) = -1
f'''(0) = 0
f''''(0) = f(0) = 1
...
1,0,-1,0을 반복함을 알 수 있다.
f(x) = cos(x)를 매클로린 전개해보자.
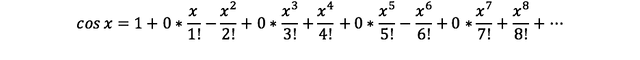
즉,
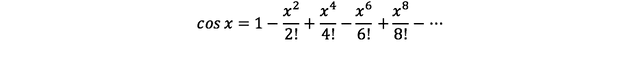
와 같이 정리할 수 있다. (#식2)
자, 숨가쁘게 왔는데, 잠시 큰 숨 들이쉬고, 조금 더 힘을 내보자.
[ Step 3 ] 거의 다 왔다. e^(ix)를 살펴보자.
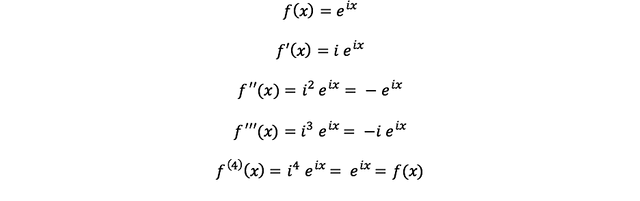
여기에도 좌우변에 x=0을 대입하면...
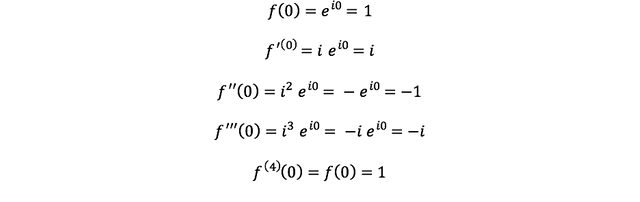
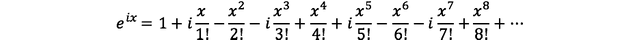
(#식3)
자...
... 자... 눈이 커지지...?
4의 주기로 cos(x), sin(x), e^(ix)가 움직이고 있고...
위 e^(ix) 는 cos(x)와 sin(x)에 i를 곱한 것의 합이라는 것을 알 수 있다....!
(식3 = 식2 + i*식1)
이라는 것을 알 수 있다.
즉, 이것이 오일러 공식이다...!!!
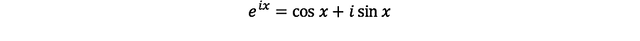
여기에 x = pi값을 넣으면
박사가 사랑한 수식을 우리도 만나볼 수 있다.
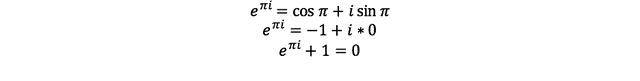
e, pi, i, -1 모두 인류가 하나씩 발견해오는 수학의 요소들인데,
이것들간의 관계가 이렇게 아름답게 연결되어있음을 발견한 오일러 스스로도 얼마나 놀랐을지 상상이 가지 않는다.
(* 오일러는 이것을 발견하고는 "이것은 창조주의 언어다..."라고 말했다고 전해지며,
농담도 잘하신다는 물리학자 고 리차드 파인만 교수님은 "the most remarkable formula in mathematics", "this is our jewel_보물"이라고 물리학 교재에 적어놓기도 하였다.)
책 혹은 영화에 나왔던 오일러 공식을 찾아가는 여정을 우리도 함께 할 수 있음에 또다른 즐거움을 느꼈기를 바라며...
[ 참고 ] 갑작스럽지만 가우스평면(Gauss Plane = Complex Plane _복소평면... 우리 말이 더 어렵다...)을 만나고 이 글을 마치자.
...-5,-4-3,-2,-1,0,1,2,3,4,5... 와 같은 실수 축에 마성의 음수 -1을 곱한다면,
축이 180도 회전하여 ...5,4,3,2,1,0,-1,-2,-3,-4,-5가 된다.
그렇다면, 제곱했을 때 -1이 되는 숫자를 i (imaginary number허수)라고 부르는데,
-1을 곱했을 때 180도 회전한다면,
i를 곱했을 때 축이 90도 회전하는 것이라고도 할 수 있지 않을까...?
라는 생각으로
가로축을 실수축, 세로축을 허수축으로 만든 평면을 가우스평면... (혹은 복소평면 Complex Plane...영어가 차라리 쉽다)이라고 한다.
즉, a+bi라는 식으로 가우스평면에 (a,b)를 편리하게 표시할 수 있다.
✅ @skyisnolimit, I gave you an upvote on your first post! Please give me a follow and I will give you a follow in return!
Please also take a moment to read this post regarding bad behavior on Steemit.
오랜만에 수학을 돌아보는시간 - ㅋㅋㅋㅋㅋ
예쓰예쓰!! 레온하르트 오일러의 업적은 정말 눈부시네요!!!