Hey steem guys!

I'm new in this social blockchain and I would like to tell you about myself.
My name is Dmitriy, I'm 23-year-old PhD student from Russia. My small motherland is Yakutia - the biggest region of Russian Federation. Its area total 3 million square kilometers. Yeah, if Yakutia were a country, she would have taken the eighth place in the list of countries by area.
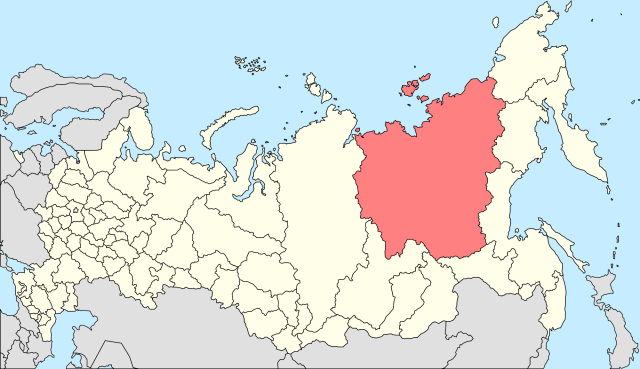
Yakutia at the map of Russian Federation
Lenskii Mountains

Nice weather for having a talk outside
I am studying In MSU (Moscow State University), my dissertation is dedicated to continuous mechanics.

(According to my Exp., people usually like the view of my University)
While I was studying at university , I went in for geometry. Actually, Higher Geometry is far not the same than the elementary geometry: it deals with objects and system symmetries as the most general conceptions. These conceptions, that I learned, help me to dive into the problems deeper, getting fulfill information.
Iterational trigonometry model.
I am interested in ML(machine learning) as well. So I look after research products of such giants of computer vision as Google, VGG, Stanford University etc.

As my hobby I like to upgrade neural networks decreasing the memory of network and increasing productivity.
To sum up, I am just fond of solving interesting problems. So, firstly I am going to post mathematical problems of middle school complexity, secondly I will explain you some interesting objects of higher mathematics (oh, by the way, I have graduated math department of my university).

Hello! I'd be interested in your thoughts on how to identify clustered data on approximate manifolds. What do you think of persistent homology in ML?
Or, what about mapping the data to Gr(K,N) and then considering the natural metric as a means for identifying data that is 'close' ?
Hello, @complexring!
What kind of obstacles can you encounter with in induced metric? In my opinion, the problem is in the quality and type of approximation.
I hardly know anything about the possible ways of applying the homology groups in machine learning, but I am quite familiar with these topological invariants. In its essence, topological invariants are a good indicator of similarity spaces / structures. Therefore, the most clear to me is their use in a exploring the features of selection of training samples.
By the way, a long time ago a teacher told me about how to determine health problem like a bowel coupler using homology. This is one of the examples of direct application of the homology groups in life. It would be fun to use homology as a means of identifying a person's identity.
What is Gr(K,N)? I can not find meaning of this term.
Sorry. Gr(K,N) is the Grassmannian where points in this spare are K-dimensional linear subspaces of an N-dimensional space.
Homology as a means of identification? As in, your personal homology is unique?
This is a bad idea because the use of non-Euclidean spaces, making it impossible to clearly determine the distance between the points. Imagine how many times you will have to solve the geodesic equation.
You can construct the model of the blood-vascular system via full body scanning and then calculate homology groups. And i think these groups can identify your person with high accuracy. Maybe using of homology is more difficult then calculating of invariants of your blood-vascular system graph.
Unfortunately, nested comments can't go on further than a depth of 6.
I just wanted to add that other techniques are taking data and using the Veronese embedding and applying Euclidean distance there. The idea here is that you have some additional info on your data, maybe it's only 20 variables and degree 8 or something, and then you can map these points under this embedding and consider the distance here. Alternatively, you can consider the inverse of this problem where you are trying to find some (approximate, possibly) generator of the ideal that defines the points on the variety.
Why would you want to restrict yourself to metrics on Euclidean spaces?
And it's not impossible to determine distance given a well-defined metric on any space. That's why it's a metric.
I'm not sure what you mean by having to solve the geodesic equation. Why is this done?
@complexring!
Sorry for a long time answer.
My message: it's may be bad idea to calculate distance between points on embedded surface as Euclidean metric. For example, take a look for sphere (Earth): Euclidean distance between north pole and south pole equal to 2R, but you can't penetrate through the Earth! You must keeping aboard surface, and, in this case, the real distance between point is equal to \pi * R.
Close point, obviously, should have similar properties, so you need to use a local metric.But of course it is necessary to take a closer look into the details of the task.e details of the task.
Welcome and enjoy the steemit life!!!
Great to have you around!
Here are some tips if you're not aware of already:
#NSFWor for#testonlyThanks, it's really helpfully!
hi @puhoshville and welcome 8]
-51.9 Celsius .... How can one survive? :D
Oh, man is a very die hard creature.
There is a joke: "in Yakutia no rappers because it is very difficult to grow up on the street"
LMFAOO!!!!
Hi, Dmitriy
Welcome on board. You'll enjoy being part of this amazing open-minded community
Welcome to Steemit! My Friend- Greeting From @dog
Awesome to have you onboard!
Welcome You to Wonderful Steemit World @xem!