On negative feedback and nutrition: Could nutritional science learn from electronic engineering?

What does electronics have to do with your health? Well, not that much when you look at it directly. But how about when we look at abstractions. Is there an abstraction that might be applicable to both electronics engineering and our struggle to find a perfect diet? In this blog post, I want to explore one abstraction from electronics engineering that could potentially be a very useful tool in figuring out your bodies responses to certain nutritional inputs and as such, help you figure out your ideal personal diet.

Much of nutritional science is either purely observational or if it isn't is done what I shall refer to as using static binary deltas in Randomized Controlled Trials.

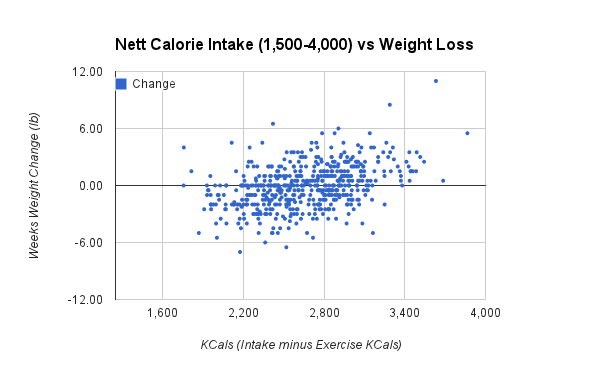
Observational studies are a great tool for hypothesis building and for showing that strong claims from other types of research are likely spurious, but at a fundamental level, observational studies, at least in nutrition, are limited in how much they can actually prove. More often than not, observational studies in nutrition will result in scatter plots that show some association with a low signal to noise ratio.

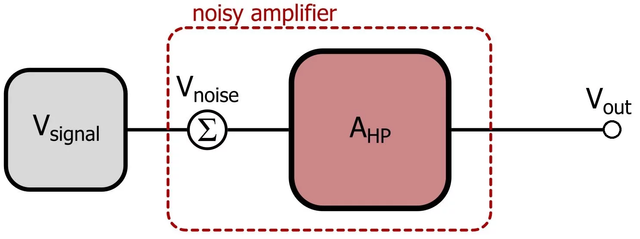
Well, while the signal may be static for individuals, the fact that we have many individuals with many input values still gives us a general abstraction of a little black box system that kind of looks like an electronics amplifier at an abstract level:

A noisy amplifier. A very noisy amplifier. Randomized Controlled Trials take a different approach. Instead of just looking at the inputs and outputs passively, a trial is designed where two randomized groups are chosen and some binary quantified artifact is used as input. This approach should reduce part of the noisiness of our black-box amplifier.

So we have what boils down to a pretty noisy amplifier that has the output response to the input, but what does that realization get us? Well, it brings us to the concept of negative feedback. I am not talking about the type of negative feedback that your superior might give you or the type of negative feedback that you might leave on Goodreads after having been disappointed in the third book of a trilogy you were reading. I am talking about negative feedback in the context of signal amplification as discovered by Harold Stephen Black.

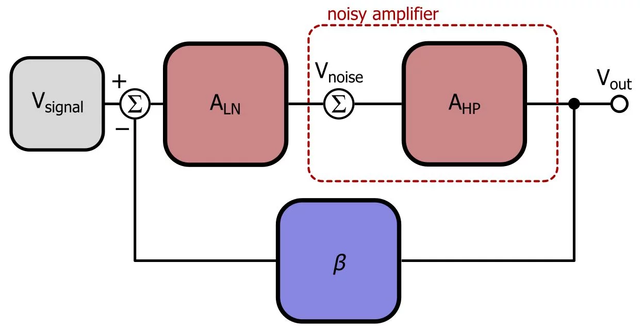
What Black discovered, in short, was that the use of a negative feedback loop allows us to trade in a bit of amplification for reduced internal noise generation by the amplifier.

So how does this help us with nutrition? Well, at first glance it doesn't. It doesn't help observational studies. It doesn't help RCT's, but what it does actually help is the often frowned upon N=1 type of approach to nutrition. That is, just like the car mechanic in an F1 racing team that won't design a new fuel injection system to make all cars run more efficiently, yet will apply his knowledge of engineering to make that one car run as fast and as efficient as possible, in the same way the use of a negative feedback loop in your personal N=1 study could help you tune your diet to something a one-size fits all scientific approach would never get you at.

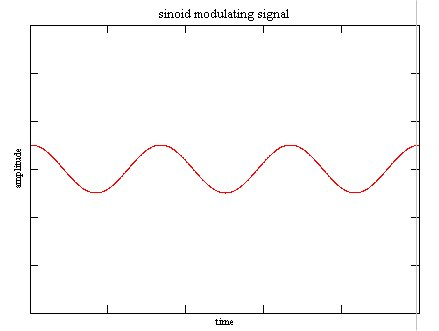
In order to do this though, we need two more components. The first thing we need is an actual input signal. Not the type of binary signal we will get in RCTs where one attribute can have only two concrete values, but we need a special type of signal in order to accommodate the final step in our journey. We need something approximating a sinoid type input signal.

For example, we could look at our protein and carbohydrate intake at stable caloric and fat intake and use a sinoid modulated protein/carb intake as input. Then if we pick a useful output signal such as relative body strength or body fat percentage as output signal. So now we have our potential noisy-amplifier. So what does dis buy us?

Well turns out that if we pick a long enough sinoid period and if our idea about a directional and responsive link between our input signal and output signal is indeed correct, then we shall be seeing some very interesting results if we introduce our negative feedback loop.

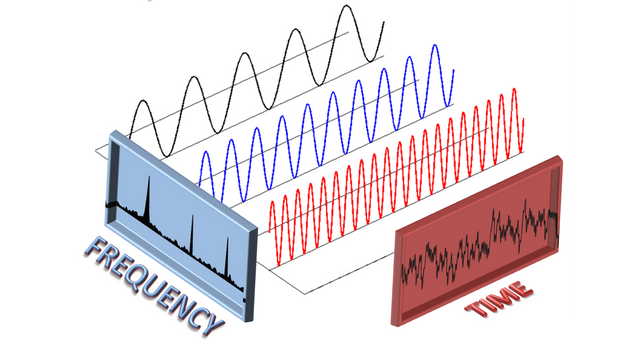
Time for the last piece of the puzzle: FFT or Fast Fourier Transform.

I won't go into the math of either negative feedback amplification or Fourier transform but the base concept is that using a simple algorithm called the Fast Fourier Transform, it is possible to get from a discrete signal (our daily output variable measurements) that is a function of the time (t) to a signal spectrum that is a function of frequency (f). This in term, given that we know the exact frequency spectrum of our input variable, allows us to estimate the signal to noise ratio for our potential amplifier.

So assuming our input variable was protein (replacing carbohydrate) and our output variable was BF% as measured on a BIA scale. Lets say our hypothesis was: More carbohydrate (when replacing protein) leads to higher BF%, then using Black's control feedback model and our FFT based signal to noise metrics, we would expect the round with negative feedback to have a higher signal to noise ratio than the reference round without a negative feedback loop.

Conversely, if instead, we observe some different dominant frequency in our output signal, this could be a sign we had our hypothesis inversed and accidentally introduced a positive feedback loop instead of a negative one.

You can repeat this experiment at different baseline levels to see how the results differ. It is quite possible that replacing carbs with protein at a 5% protein base level could yield amazing results yet at a 35% protein base level could yield zero or even negative results, leading to accidental positive feedback loops as described above.

Please note that this is just the preliminary research part of the applicability of control feedback theory to diet and workout in an N=1 engineering setting. Ones you have figured out the important factors, it could become theoretically possible to design a multivariate control feedback system for your own body. Doing so was supposed to be a main subject in my now abandoned book writing ambitions. Efforts I abandoned largely due to what seem to be hysteresis effects that got in the way of effective multivariate control feedback design using my modest math skill set.

So would negative feedback loops used in this way be suitable beyond the N=1 engineering setting? I am not a scientist, at least not by trait, I'm an engineer. With that disclaimer, however, and given my knowledge on data science, epistemology and causality reasoning, I don't actually see any reason why you couldn't do RCTs where one group is given theorized negative feedback applied to the input signal where the other group isn't. But then, if there is no reason why it couldn't be done, I also see no reason why it isn't actually being done in an any way pervasive enough way to make its mark on the literature. It is not as if Black's work on control feedback has ever been in any way obscure, so there might be some caveat with its applicability to RCT that I am missing. If there is,I would love to hear from you.