Programación en lenguaje ensamblador para el RISC-V
Soy estudiante de ingeniería electrónica de la Universidad Simón Bolívar de Venezuela (USB), hace unos meses me encontraba cursando la materia “Arquitectura del computador 2” donde se nos estuvo evaluando la elaboración de programas en lenguaje “Assembler” a través del rars.
Objetivos:
Escribir un código en lenguaje ensamblador que realice la multiplicación con signo de números de 32-bits, sin usar ninguna instrucción de multiplicación, el resultado debe ser un numero de 64-Bits. Utilizar el “Algoritmo de Booth”.
Implementación y desarrollo:
Se tomó como base el “Algoritmo de Booth”.
1) Se determinan los valores de A, S y el valor inicial de P. Todos de 64 bits más uno extra.
A: Se llenan los 32 bits más significativos (MSB) con el valor de Multiplicando, el resto, con ceros.
S: Se llenan los MSB con el valor de “Menos multiplicando” en notación de complemento a dos, el resto, con ceros.
P: Se llenan los 32 (MSB) con ceros. A la derecha, se llenan los Bits menos significativos (LSB) con el valor de multiplicador. El bit extra, es 0.
2) Se determinan los dos bits menos significativos de P y se distinguen los casos.
• Si son 01, P = P + A. Ignorar overflow.
• Si son 10, P = P + S. Ignorar overflow.
• Si son 00 o 11, no hacer nada.
3) Se hace shift aritmético a la derecha, por un espacio, del valor obtenido en el paso anterior. Este será el nuevo P.
4) Se repiten los pasos 2 y 3 por 32 veces.
Para ilustrar el proceso se adaptó el algoritmo para trabajar con la siguiente tabla:

Texto

Al empezar la operación se compara el multiplicador con una de las constantes declaradas cuyo valor es uno, para determinar si el penultimo numero es uno o cero. De resultar “1”, nos dirigiremos a la funcion “Uno_Y_Algo” donde se determinará el bit extra para concluir en que caso nos encontramos, dependiendo el resultado se realiza la acción indicada en la descripción del algorirtmo, para asi llegar a la funcion “ShiftDerecho”. Dependiendo de los resultadoas anteriores, se cambia o no el bit extra. Luego, para aplicar el shift, se toman en cuenta los LSB de S2 y S3. Si alguno de ellos es 0, se aplica shift tanto a él como al registro de su derecha. Si el de S2 es 1, a S3 se le hace shift y XOR con 0x80000000. De no caer en la función “Uno_Y_Algo” o “Cero_Y_Uno” para posteriormente llegar a “ShiftDerecho” y proceder como en el caso anterior.
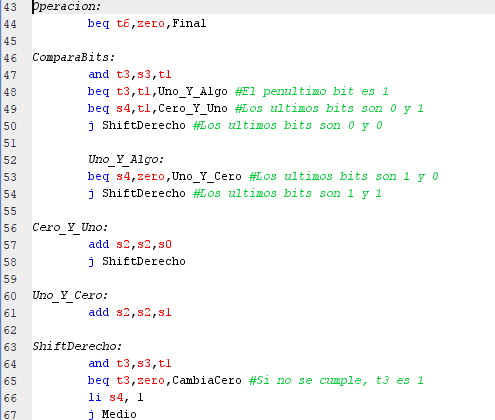
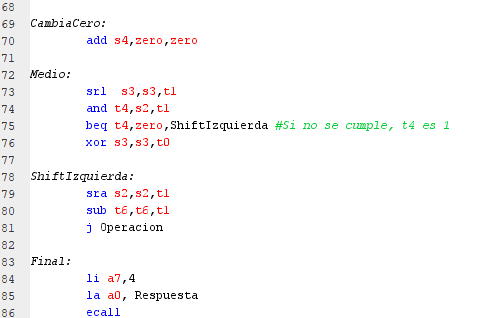
Cuando el contador de bits llega a cero se procede a la función “Final” en la cual se imprime el resultado en hexadecimal, de los dos registros S2 y S3. Ya que un número muy grande no sería visible.
Resultados:
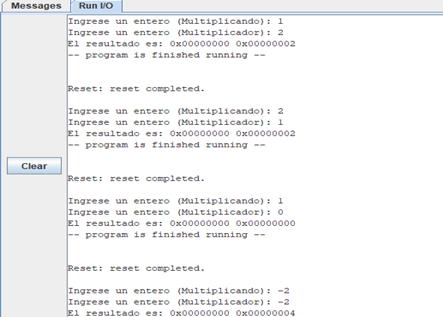
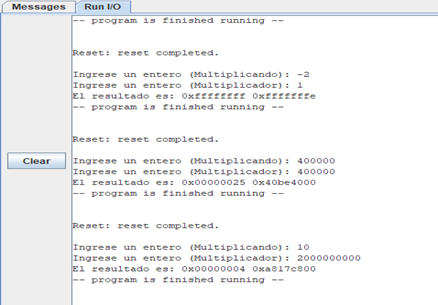
Se comprobó el correcto funcionamiento de las multiplicaciones para diferentes casos; incluyendo multiplicación por cero, propiedad conmutativa, números negativos y números más grandes, obteniendo los resultados esperados.
Conclusiones:
Se puede observar que el código funciona según lo requerido ya que se realiza la operación pedida sin arrojar algún error o incongruencia.
Referencias:
Terrones Angel, “A1” archivo entregado en octubre de 2019.
Asanovic, K.; Waterman A. “The RISC-V Instruction Set Manual, Volume I: User- Level ISA” (2017) 2CS Division, EECS Department, University of California, Berkeley.
“Algoritmo de multiplicación de cabina” titulo disponible en: https://en.wikipedia.org/wiki/Booth%27s_multiplication_algorithm Fecha de consulta, octubre de 2019.
“Multiplicación. Algoritmo de Booth” Titulo disponible en: https://www.emezeta.com/articulos/multiplicacion-algoritmo-de-booth Fecha de consulta, octubre de 2019.
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @minnowbooster.
If you appreciate the work we are doing, then consider supporting our witness @stem.witness!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider using the steemstem.io app and/or including @steemstem in the list of beneficiaries of this post. This could yield a stronger support from SteemSTEM.