[수학 이야기 #3-1] 술에 취한 사람은 집에 들어갈 수 있을까? 무작위 행보 (random walk) [1편]

mathsolver (53)in #kr • 6 years ago (edited)

[1]

술에 취한 사람이 돌아오는 이유? [1편]

우스갯소리로 하는 말이지만, 이것을 수학적으로 분석해서 어느정도 (?) 맞는 말 임을 보일 수 있다.

1. 무작위 행보 (Random Walk)란 ? - [2]

어떠한 물체가 유클리드 공간 $\mathbb{R}^d$ 상 원점 $O(0, 0, ..., 0)$ 에서 시작해서, 다음과 같은 규칙으로 움직인다 생각해보자. $n$ 번째 단계에서의 물체의 위치를 $X_n$ 라 하면,

Step 1. $X_0 = (0, 0, ... ,0)$ (시작점)

Step 2. 단위 벡터

$e_j = (0,...,0, \underbrace{1}_{j-th}, 0, ...,0)$
에 대해,
$X_{n+1} = X_n \pm e_j$ 일 확률이 모든 $j = 1, 2, ..., d$ 에 대해

$\frac{1}{2d}$

로 동일하게 주어짐.

예를 들어서

$d=1$ 차원이라면, 수직선 위 원점에서 시작하여 오른쪽 또는 왼쪽으로 (각각 확률 1/2을 부여) 움직이는 운동을 말한다.
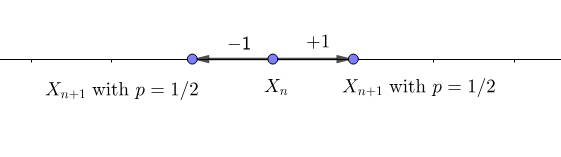
$d=2$ 차원 이라면, 원점에서 시작하여 동, 서, 남, 북 으로 (각각 확률 1/4을 부여) 움직이는 운동을 말한다.
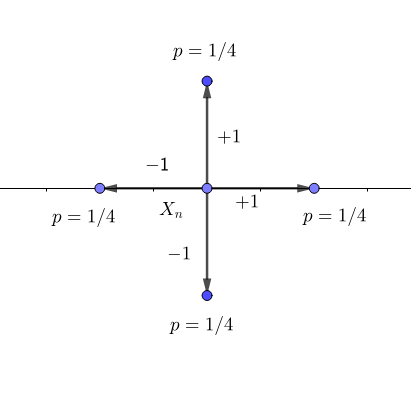
마지막으로 $d=3$ 차원 이라면, 원점에서 시작하여 동, 서, 남, 북, 상, 하 방향 으로 (각각 확률 1/6을 부여) 움직이는 운동을 말한다.

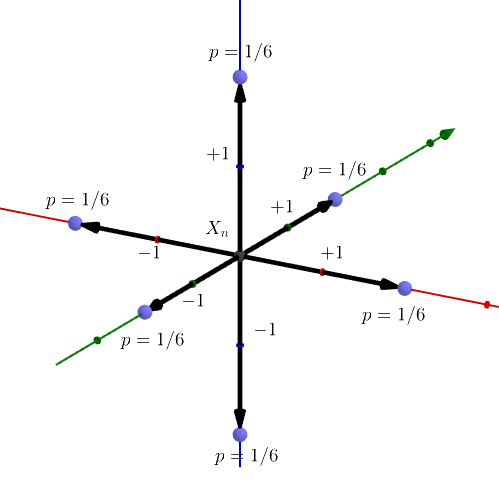
즉 원점에서 시작한 운동은 항상 좌표들이 정수인 격자점 만을 거친다고 보는 것이다. 그렇다면 이 모델이 술 취한 사람이 다시 집으로 돌아오는 것과 무슨 연관이 있을까?

2. 1차원에서의 무작위 행보

일단 가장 간단한 1차원에서의 Random Walk를 살펴보자. 다음은 $n = 100$ 까지 Python을 이용하여 Random Walk를 구현한 뒤, 각 단계에서의 좌표값을 조사한 예시이다.

import matplotlib.pyplot as plt
import numpy as np

def random_walk_1D(n):
    elements = [1, -1]
    probabilities = [0.5, 0.5]
    x = [0]
    for i in range(1, n + 1):
        y = np.random.choice(elements, 1, p = probabilities)
        x.append(x[i-1] + y)    
    return x
#----------------------#
n = 100
N = [i for i in range(n+1)]

plt.plot(N, random_walk_1D(n))
plt.grid(axis = 'y')
plt.xlabel('n')
plt.ylabel('$X_n$')
plt.show()

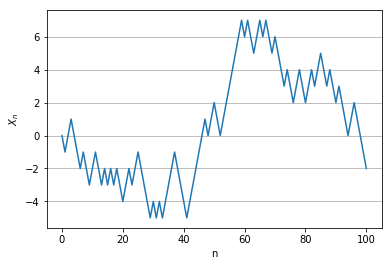
술에 취한 사람이 집으로 돌아온다는 것은 Random Walk를 시행하는 도중 $X_n = 0$ 이 되는 상황을 의미하므로, $X_n = 0$ 이 발생하는 상황에 대한 조사를 시행하면 될 것이다.

2-1. 언제 원점으로 돌아오는가?

$n$ 번의 시행 중 오른쪽으로 간 횟수를 $x$ , 왼쪽으로 간 횟수를 $y$ 로 놓자. 만약 $X_n= 0$ 라면, 다음을 만족해야 한다.

$x +y = n, x - y = 0 \implies n = 2x$

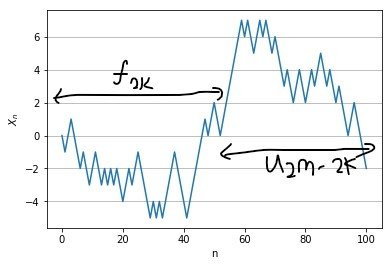
따라서 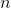$n$ 이 짝수일 때만 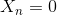$X_n = 0$ 이 될 수 있다.

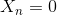2-2. $X_n = 0$ 일 확률은?

이제 짝수 $n$ 이 주어졌다고 가정하고, $X_n = 0$ 일 확률 $u_{n}$ 을 구해보자. 이는 바로 위 Section 2-1에서 알 수 있듯이

$x = y = n/2$

이므로 $n = 2m$ 으로 놓는다면

$u_n={n \choose n/2}2^{-n} =u_{2m} = {2m \choose m}2^{-2m}$

이 나온다. (편의상 $u_0 = 1$ 로 놓자.)

2-3. 처음으로 원점을 찍는 경우? - [3]

Section 2-1의 예시로 돌아가보자. 그래프를 보면 100번의 시행에서 원점으로 되돌아 가는 상황은 정확히 (초기값을 제외하면) 7번 나왔다.

술에 취한 사람이 집을 잘 찾아가놓고 6번이나 다시 집을 나온다?

우스꽝스러운 상황이 아닐 수 없다.

집을 한번 들어가면 그걸로 끝이지 다시 집을 나온 뒤 되돌아감을 반복하는 상황은 우리가 원하던 바가 아니다. 따라서 새로운 변수를 정의해야한다. $n = 2m$ (짝수)에 대해, 다음과 같이 정의한다.

$f_n = f_{2m}$ 은 $(X1_{2m} = 0)$ 을 만족하고 모든 $k < n=2m$ 에 대해 $X_k \neq 0$ 를 만족할 확률

즉 $n$ 보다 작은 경우 원점으로 되돌아가는 일이 없어야 한다. 편의 상 $f_0 = 0$ 로 놓고, $u$ 와 $f$ 간의 관계를 알아보자.

$u_{2m}2^{2m}\ (m \geq 1)$ 은 원점에서 시작해 $X_{2m} = 0$ 를 만족하는 모든 Random Walk 경로의 수를 뜻한다. 이러한 경로들은 처음으로 원점을 찍는 위치 $2k (\leq 2m)$ 에 의해 분할 (partition) 된다. $2k$ 에서 처음으로 원점을 찍는 경로의 수는 정의에 의해

$(f_{2k}2^{2k}) \times (u_{2m-2k}2^{2m-2k}) = f_{2k}u_{2m - 2k} 2^{2m}$

를 만족한다.

$k = 0, 1, ..., m-1, m$ 를 모두 합하면,

$u_{2m} = f_0 u_{2m} + f_{2}u_{2m-2} + ... + f_{2k}u_{2m-2k} + ... + f_{2m}u_0$

3. 생성함수를 이용하여 분석하기

3-1. 생성함수와 이항정리

우리가 2-2에서 정의한 $u_{2m}$ 과 2-3에서 정의한 $f_{2m}$ 을 수열

$\left\{ u_{2m} \right\} = \left\{ \tilde{u}_m \right\}, \left\{ f_{2m} \right\} = \left\{ \tilde{f}_m \right\}$

로 본다면, 이들의 생성함수는 다음과 같다.

$\tilde{U}(x) = \sum_{m=0}^{\infty} \tilde{u}_m x^{m},\ \tilde{F}(x) = \sum_{m=0}^{\infty} \tilde{f}_mx^{m}$

다항식의 코시곱을 떠올려보면 Section 2-3에서 나온 식을 적용해볼 수 있다.

$\begin{align*} \tilde{U}(x) &= 1 + \sum_{m=1}^{\infty} \tilde{u}_m x^m \\ &= 1 + \sum_{m=1}^{\infty} (\tilde{f}_0 \tilde{u}_m + ... + \tilde{f}_m \tilde{u}_0)x^{m} \\ &= 1 + \left( \sum_{j=0}^{\infty} \tilde{f}_j x^{j} \right) \left( \sum_{k=0}^{\infty} \tilde{u}_k x^k \right ) \\ &= 1 + \tilde{F}(x)\tilde{U}(x) \end{align*}$

따라서 $\tilde{F}(x) = \frac{\tilde{U}(x)}{\tilde{U}(x) - 1}$ 을 만족한다. $\tilde{u}_m = u_{2m} = {2m \choose m}2^{-2m}$ 이므로 이항정리 (Binomial Theorem) - [4] 에 의해

$\tilde{U}(x) = \frac{1}{\sqrt{1-x}}\ (\text{where }x \in (-1, 1))$

이 성립한다. 따라서

$\tilde{F}(x) = 1 - \frac{1}{\sqrt{1-x}}\ (\text{where }x \in (-1, 1))$

이다. 함수식에서 직접 계산을 통해

$\tilde{F}'(x) = \tilde{U}(x)/2 \implies f_{2m} = \frac{u_{2m}}{2m-1}\ (m \geq 1)$

임을 알 수 있다.

3-2. 결과

다시 돌아가서 우리의 원래 문제로 가보자. 술에 취한 사람이 집에 들어오면 다시 나가는 경우를 배제하였으므로,

술에 취한 사람이 반드시 집으로 다시 돌아오는가?

에 대한 답은 확률의 무한 합

$f_{\infty} = \sum_{m=0}^{\infty} f_{2m}= f_2 + f_4 + f_6 + ... + f_{2m} + ... = 1$

을 증명하는 것과 동치이다! 먼저, $f_{2m} > 0$ 이고 부분합들은 $1$ 을 상한으로 가지니 (bounded above by 1) 수렴함은 분명하다. 스털링 근사 [5] 에 의해 충분히 큰 자연수 $N$ 와 상수 $K$ 에 대해

${2m \choose m} \leq K \frac{4^{m}}{\sqrt{\pi m}}\ (\forall m \geq N)$

이 성립하므로

$\begin{align*} \sum_{m=0}^{\infty} f_{2m} &= \sum_{m=0}^{N-1}f_{2m} + \sum_{m=N}^{\infty}\frac{u_{2m}}{2m-1} \\ &\leq \sum_{m=0}^{N-1}f_{2m} + K \sum_{m=N}^{\infty} \frac{4^m 2^{-2m}}{\sqrt{\pi m}(2m-1)} \\ &= \sum_{m=0}^{N-1}f_{2m} + \frac{K}{\sqrt{\pi}} \sum_{m=N}^{\infty} \frac{1}{m\sqrt{m}} <\infty\end{align*}$

무한합은 수렴한다.

따라서, 생성함수의 극한에 대입하면

$f_{\infty} = \lim_{x \rightarrow 1^-} F(x) = 1$

이 나온다!

4. 결론

무작위 행보 (random walk) 이론을 대입해서 나온 결론은 다음과 같다. 원점에 위치한 집을 나온 상태에서 술에 취한 사람이 언젠가 다시 집으로 돌아갈 확률은 1차원 의 경우 1이다. 즉 언젠가는 반드시 집으로 돌아간다. 물론 이를 왜곡해서 해석하면 안된다.

가령, 우리가 random walk의 시행 횟수를 정해놓았을 경우, 그 시행의 횟수 내에서 반드시 원점으로 돌아감을 보장하지는 않는다. 시행의 횟수가 유한하지 않고, 무한히 늘릴 경우 (즉 $m \rightarrow \infty$ ) 에만 해당함에 주의하자. 물론 현실에서는 계속 돌아다니다 보면 동사하거나 누군가가 집으로 데려다 주겠지만 어쨌든 이렇다는 거다 ㅋㅋ.