Linear Program Mathematics
A building parking lot has an area of 400 m2. To park a car required area of 10 m2 and for bus 15 m2. Totol parking lot can only accommodate a total of 20 vehicles. If the parkirmobil tariff is Rp5,000 / hour and the bus is Rp.7500 / hour, what is the maximum income from the parking service if it is assumed in one hour no vehicles are in and out?
The above is an example of a solution that uses a linear program. Before studying linear programming in high school, you must first have understanding about incidences and graphics. It will often be used in applying linear progaram to find out the result area of a function. The material on the 12th grade linear program is quite interesting and easy to understand. The questions must also come out in the national exam.
Linear Inequality TwoVariabel
This inequality is generally written in form
ax + by ≤ c or ax + by ≥ c in linear programming material will often appear a mathematical sentence that must be translated into the form of inequality above. You should then describe it in the cartesius field and determine the result region. The inequality has a settlement of the set of pairs (x, y) that satisfies the inequality. Well the settlement form can be drawn in cartesius field coordinates and the result is a hatchery.
Problems example
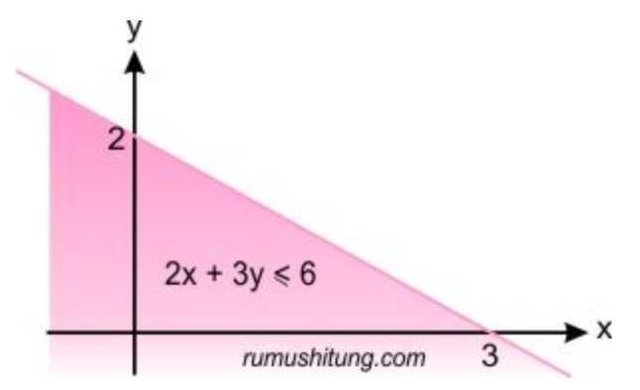
Determine the settlement of the inequality 2x + 3y ≤ 6
Alternative way to answer it
Step 1 line drawing 2x + 3y = 6 on the diagram cartesius by first pinpointing the intersection point on the x axis of the intersection of the x axis (y = 0) 2x + 3y = 6 2x + 0 = 6 x = 3 → (3.0) (x = 0) 2x + 3y = 6 0 + 3y = 6 y = 2 → (0,2) the image of the garage appears The line equation image
Step 2 Calculate buddy note the sign of inequality and coefficient x to determine the shading area. Try entering the value of x (eg 0) if it satisfies the equation then the side of the area where point x = 0 is the result area.
inequality in linear programming
What is a Linear Program?
The so-called program linear is a set of rules in which there is a linear function as a function of purpose and a linear inequality system that acts as a boundary (limiting function). The linear program for duavariables is written:
The function that produces the maximum value f (x, y) = c1x + c2y with the limits a1x + b1y ≤ c a2x + b2y≤ c with x ≥ and y ≥ 0 Now the question is, "How to find the x and y points that generate the maximum value? "Check this ouuut ...: D
Determining the Maximum Value of Purpose Functions in the Linear Program
To determine the maximimax of the linear program problem you can use the way by depicting the graph of the inequalities that exist. Here are the steps:
Determine the set of settlements of each inequality then check the result area in cartesius diagram
Look for extreme points
Determine the result or value of the function of each extreme and you will find the maximum value
Example:
Find the maximum value of the function f (x, y) = 3 x + 5 y with the restriction 3x + y ≤ 6 x + 2y ≤ 4 x ≥ and y ≥ 0
Answer:
We illustrate the result of the unequal 3x + y ≤ 6 and x + 2y ≤4 in the cartesius diagram
Inequality Point Cut Sb x Point Cut Sb y
3x + y ≤ 6 (2.0) (0.6)
x + 2y ≤ 4 (4.0) (0.2
By using what we described earlier then in can images:
We find the point B that is the intersection point of the two differentiation using the method of elimination (or substitution)
3x + y = 6 [x 2] ⇒ 6x + 2y = 12
x + 2y = 4 [x 1] ⇒ x + 2y = 4
5x = 8 --------------------
x = 8/5
x + 2y = 4
8/5 + 2y = 4
2y = 4 - 8/5 = 20/5 - 8/5 = 12/5
y = 6/5
From the cartesiustersebut diagram get the extreme point
O (0,0); A (2.0); B (8 / 5.6 / 5); C (0.2)
The value of f (x, y) = 3 x + 5 ykita search for each extreme point
f (O) = 0 + 0 = 0
f (A) = 3 (2) + 5 (0) = 6
f (B) = 3 (8/5) + 5 (6/5) = 54/5 = 10 4/5
f (C) = 3 (0) + 5.2 = 10
So the maximum value of the objective function is 10 4/5 obtained at the point (point) B (8 / 5.6 / 5)
example about linear program
Using Survey lines
In the maximum nilaimaksimum program of a function the actual objective can be searched with the help of the line of sight. How to? Buddy the first image of the line of purpose function f (x, y). Then slide the line at the extreme points of the barrier inequality. Observe where, when the garriselidik positions and the result areas of the inequality produce the most resulted areas below the line of inquiry. That's what's called the maximum point.
Matematika Program Linier
Sebuahtempat parkir gedung punya luas 400 m2. Untukmemarkir sebuah mobil diperlukan luas 10 m2 danuntuk bus 15 m2. Totol tempat parkir tersebuthanya bisa menampung kendaran berjumlah 20 buah. Jika tarif parkirmobil adalah Rp5.000/jam dan bus adalah Rp.7500/jam, berapa pendapatanmaksimal dari jasa parkir tersebut jika diasumsikan dalam satu jamtidak ada kendaraan yang masuk dan keluar?
Soal di atas adalah contohsoal yang penyelesaiannya menggunakan program linier. Sebelum belajarprogram linier di SMA, sobat harus terlebih dahulu punya pemahamantentang petidakasmaan dan juga grafiknya. Ia akan sering dipakai dalamaplikasi soal progaram linier untuk mengetahui area hasil dari suatufungsi. Materi tentang program linier SMA kelas 12 cukup menarik danmudah untuk dipahami. Soal-soalnya juga pasti keluar dalam ujiannasional.
Pertidaksamaan Linier DuaVariabel
Pertidaksamaan ini secaraumum ditulis dengan bentuk
ax+ by ≤ c atau ax + by ≥ c dalam materi program linier akansering muncul kalimat matematika yang harus sobat terjemahkan ke dalambentuk pertidaksamaan di atas. Selanjutnya sobat harus bisamenggambarkannya dalam bidang cartesius dan menentukan daerah hasilnya.Pertidaksamaan tersebut mempunyai penyelesaian berupa himpunan pasangan(x,y) yang memenuhi pertidaksamaan. Nah bentuk penyelesaiannya dapatdigambarkan dalam koordinat bidang cartesius dan hasilnya merupakandaerah arsiran.
Contoh Soal
Tentukan penyelesaian daripertidaksamaan 2x + 3y ≤ 6
Alternatif cara menjawabnya
Langkah 1gambar garis 2x + 3y=6 pada diaragm cartesiusdengan terlebih dahulu meneetukan titik potongnya pada sumbu x maupaunytitik potong sumbu x (y=0) 2x + 3y=6 2x + 0=6 x=3 → (3,0) titikpotong sumbu y (x=0) 2x + 3y=6 0 + 3y=6 y=2 → (0,2) gambar garitersebut tampakGambar persamaan garis
Langkah 2Sobat hitung perhatikan tanda pertidaksamaan dankoefisien x untuk menentukan daerah arsiran. Cobalah memasukkan nilai x(misal saja 0) jika memenuhi persamaan maka sisi area dimana titik x=0 berada merupakan daerah hasil.
pertidaksamaan dalam program linier
Apa Itu Program Linier?
Yang dinamakan programlinier adalah sebuahkumpulan aturan yang di dalamnya terdapat sebuah fungsi linier sebagaifungsi tujuan dan sebuah sistem pertidaksamaan linier yang berperansebagai batas (fungsi pembatas). Program linier untuk duavariabel ditulis:
Fungsi yang menghasilkan nilai maksumum f(x,y)=c1x+ c2y dengan batasan a1x+ b1y ≤ c a2x + b2y≤ c dengan x ≥ dan y ≥ 0 Sekarang yang menjadi pertanyaan adalah,"Bagaimana menemukan titik x dan y yang menghasilkan nilai maksimum?"Check this ouuut... :D
Menentukan Nilai MaksimumFungsi Tujuan dalam Program Linier
Untuk menentukan nilaimaksimal dari soal program linier sobat dapat menggunakan cara denganmenggambarkan grafik dari pertidaksamaan yang ada. Berikutlangkah-langkahnya :
Tentukan himpunan penyelesaian dari tiap pertidaksamaanlalu sobat gambarkan daerah hasilnya di diagram cartesius
Cari titik-titik ekstrim
Tentukan hasil atau nilai dari fungsi masing-masing titikekstrim dan sobat akan menemukan nilai yang maksimum
Contoh :
Tentukan nilai maksimum dari fungsi f(x,y)=3 x + 5 y dengan batasan3x + y ≤ 6 x + 2y ≤ 4 x ≥ dan y ≥ 0
Jawab :
Kita gambarkan derah hasil dari pertidak samaan 3x + y ≤ 6 dan x + 2y ≤4 pada diagram cartesius
Pertidaksamaan TitikPotong Sb x TitikPotong Sb y
3x+ y ≤ 6 (2,0) (0,6)
x+ 2y ≤ 4 (4,0) (0,2
Dengan menggunakan yangtelah kami jelaskan sebelumnya maka di dapat gambar :
Kita tentukan titik B yangmerupakan titik potong dua pertidaksamaann menggunakan metode eliminasi(bisa juga substitusi)
3x + y=6 [x 2] ⇒ 6x + 2y=12
x+ 2y=4 [x 1] ⇒ x + 2y=4
5x=8 --------------------
x=8/5
x + 2y=4
8/5 + 2y=4
2y=4 - 8/5=20/5 - 8/5=12/5
y=6/5
Dari diagram cartesiustersebut sobat dapatkan titik ekstrim
O (0,0) ; A (2,0) ; B (8/5,6/5) ; C (0,2)
Nilai f (x,y)=3 x + 5 ykita cari untuk masing-masing titik ekstrim
f(O)=0+0=0
f(A)=3(2) + 5(0)=6
f(B)=3(8/5) + 5(6/5)=54/5=10 4/5
f (C)=3(0) + 5.2=10
Jadi nilai maksimal dari fungsi tujuan adalah 10 4/5 yang didapat padakondisi (titik) B (8/5,6/5)
contoh soal program linier
Menggunkan Garis Selidik
Dalam program linier nilaimaksimum dari suatu fungsi tujuan sebenarnya dapat dicari denganbantuan garis selidik. Bagaimana caranya? Sobat gambar dulu garis darifungsi tujuan f(x,y). Kemudian geser garis tersebut pada titik-titikekstrim pertidaksamaan pembatas. Amatilah di mana ketika posisi garisselidik dan daerah hasil dari pertidaksamaan menghasilkan daerah hasilyang paling banyak berada di bawah garis selidik. Itulah yang disebuttitik maksimum.
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by fatimahzaini from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.