ESTUDIO DE LA INFLUENCIA DEL PERÍODO NATURAL DE UNA ESTRUCTURA Y DEL FACTOR DE REDUCCIÓN DE RESPUESTA CEDENTE EN LOS NIVELES DE DUCTILIDAD QUE ESTA DESARROLLA A TRAVÉS DE ESPECTROS DE RESPUESTAS INELÁSTICOS
INTRODUCCIÓN
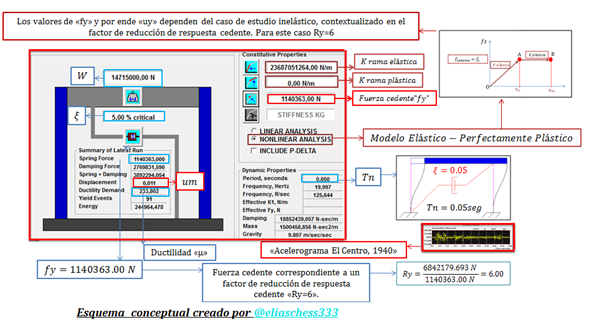
A continuación vamos a profundizar en la influencia que tiene el período natural “Tn” y el factor de reducción de respuesta cedente “Ry” en el comportamiento inelástico de una estructura, cuantificado en función de la demanda de ductilidad “μ” desarrollada una vez la estructura supere el nivel de cedencia. Recomiendo la lectura de la referencia N°04, donde se abordan conceptos que se derivan del análisis inelástico de las estructuras, entre los que destacan: fuerza cedente “fy”, desplazamiento cedente “uy”, modelos elásticos-perfectamente plásticos, entre otros; no obstante, en el tópico concerniente a “BASES CONCEPTUALES QUE ORIENTAN EL TRABAJO”, se realizará una breve explicación de los mismos. Apreciemos el esquema conceptual de la imagen N°01, para así tener una visión general de los contenidos a estudiar.
Imagen N°01: ideas generales a estudiar
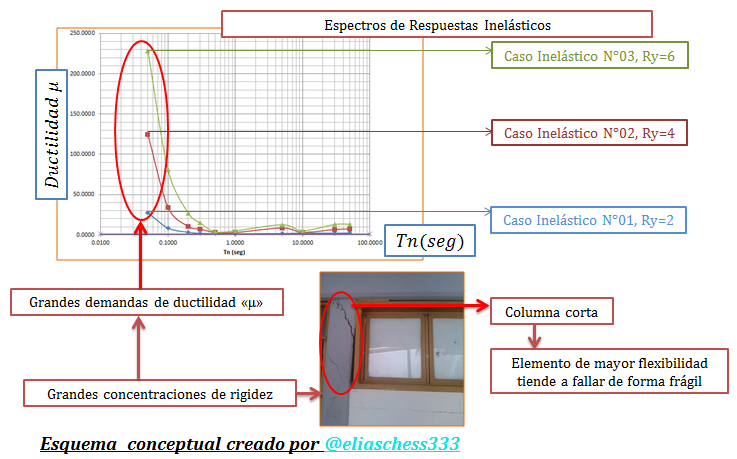
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Las imágenes corresponden al Complejo Académico Los Perozo, Coro-edo. Falcón y las mismas fueron capturadas con mi dispositivo Tablet VIT-T4000. El gráfico que se presenta fue elaborado con la herramienta computacional Microsoft Excel, con data proveniente de la herramienta computacional NONLIN V 7.14.
Tal como se aprecia en la imagen N°01, los espectros de respuestas inelásticos que estaremos utilizando para lograr con el propósito de este artículo, serán construidos graficando en el eje de las ordenadas los valores de ductilidad “μ” y en las abscisas los valores de periodo natural “Tn”. Este tipo de espectros, nos permiten apreciar de modo muy didáctico, las grandes demandas de ductilidad “μ” que experimentan los sistemas extremadamente rígidos cuando se supone un estado de cedencia en los mismos, el cual se encuentra condicionado al mismo tiempo al factor de reducción de respuesta cedente “Ry”.
DELIMITACIÓN DE LA TEMÁTICA A ESTUDIAR
La estructura tomada como referencia está representada por un pórtico plano, cuyas columnas están imposibilitadas de deformarse axialmente (área infinita) y las vigas son idealizadas como cuerpos infinitamente rígidos (área infinita e inercia infinita), lo que le confiere un grado de libertad tanto estático como dinámico. Dado que una de las variables a estudiar está representada por el período natural “Tn” se definen para tal fin diez sistemas estructurales, dejando en todos ellos constante la fracción de amortiguamiento crítico “ξ”.
Imagen N°02: sistemas estructurales con sus respectivos valores de período natural “Tn”
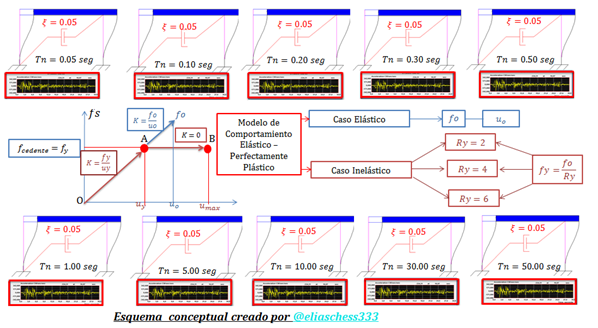
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Paint y AutoCAD V 2007. Los gráficos resaltados en color “rojo” provienen de una captura de pantalla realizada a la herramienta computacional NONLIN V 7.14.
La otra variable a considerar es el factor de reducción de respuesta cedente “Ry”, donde se plantean varios casos de comportamiento inelásticos como los ilustrados en la imagen N°01. Ahora bien, el estudio de tales variables en la influencia de los valores de ductilidad por medio de la construcción de espectros de respuestas inelásticos, sugiere reflexionar sobre los principales componentes que constituyen la ecuación de equilibrio dinámico del sistema estructural, desarrollada con un enfoque alternativo, cuya deducción puedes encontrar en la referencia N°04, la cual da por resultado lo siguiente:
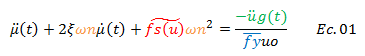
Con el propósito de lograr una mejor comprensión conceptual de esta ecuación, vale la pena adecuarla en función de las variables a estudiar; en este sentido analicemos en primera instancia los términos resaltados en la misma. Se tiene que el término resaltado en color “rojo”, representa la relación entre la función que rige la fuerza de restitución elástica “fs(u)” con respecto a la fuerza cedente “fy” y viene dado por:
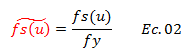
Por su parte el término resaltado en color “verde” de la ecuación N°01, es la excitación del terreno, representada en este estudio por el “Acelerograma El Centro, California, 1940”. El término resaltado en color “azul” se conoce como fuerza cedente normalizada, y relaciona la fuerza cedente “fy” con respecto a la fuerza máxima que soporta un sistema elástico “fo” , tal como se aprecia en la ecuación N°03:
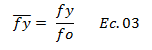
Para los fines de este artículo, estaremos trabajando con el recíproco de la fuerza cedente normalizada, conocido como factor de reducción de fuerza cedente “Ry”, el cual viene dado por:
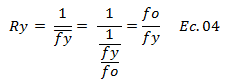
Por lo que la fuerza cedente normalizada puede ser expresada como:
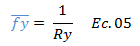
Dado que estaremos centrando la atención en la influencia del período natural “Tn” sobre los niveles de ductilidad “μ” que la estructura pueda desarrollar, conviene traer a colación la siguiente expresión:
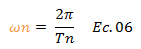
Al sustituir la ecuación N°02, N°05 y N°06 en la ecuación N°01 obtenemos lo siguiente:
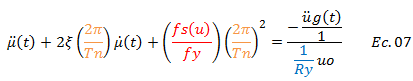
Rescribimos:
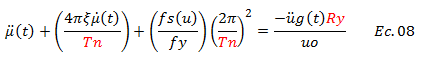
Esta forma alternativa del planteamiento de la ecuación diferencial de equilibrio dinámico del sistema estructural, permite resaltar didácticamente las variables que consideraremos en la estimación de la demanda de ductilidad “μ” ante la excitación sísmica “üg(t)”, dichas variables se encuentran resaltadas en color “rojo”. La ecuación N°08 se resolverá numéricamente con ayuda de la herramienta computacional NONLIN V 7.14. Vale destacar que trabajaremos con distintos valores de periodo natural “Tn”, haciendo un recorrido por estructuras muy rígidas (“Tn” muy bajo) hasta llegar a estructuras muy flexibles (“Tn” muy alto) (ver imagen N°02). En lo que respecta al factor “Ry”, tomaremos como referencia los siguientes casos de estudios:

En los análisis a desarrollar es importante la respuesta elástica en el tiempo, obtenida con ayuda de la herramienta computacional NONLIN V 7.14 para cada valor de periodo a estudiar, extrayendo los valores máximos de fuerza y desplazamiento “fo y uo” , y a partir de allí con el uso de la ecuación N°09 definir la fuerza cedente “fy” de conformidad con el caso inelástico de estudio, la cual nos permitirá incluir la condición inelástica en la herramienta computacional NONLIN V 7.14, como se aprecia en los esquemas conceptuales de las imágenes N°04, N°05 y N°06.
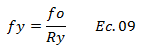
Para los propósitos de este artículo, la respuesta estructural estará contextualizada en los valores de ductilidad “μ” que se alcanzan para cada caso de estudio inelástico, donde es de vital importancia el conocimiento de los desplazamientos máximos “um” y cedentes “uy”, de los distintos modelos estructurales que se analizarán, derivándose toda una gama de información con la que estaremos construyendo los espectros de respuestas inelásticos; y así de un modo gráfico, facilitar la comprensión de la influencia de “Tn” y “Ry” en los valores concernientes a demanda de ductilidad “μ” y al mismo tiempo de los términos que constituyen la ecuación N°01. Recomiendo al lector la revisión de la referencia N°05, donde se aborda el tema de construcción de espectros desde un punto de vista del comportamiento elástico de la estructura, lo cual es base para adentrarnos en el planteamiento de espectros de respuestas inelásticos.
BASES CONCEPTUALES QUE ORIENTAN EL TRABAJO
En primera instancia, es conveniente precisar que una vez el modelo estructural en estudio entra en el rango de comportamiento inelástico, producto de la excitación sísmica, y para un determinado valor de cedencia, estaremos considerando una distribución de esfuerzos elástica-perfectamente plástica como se aprecia en el gráfico del esquema conceptual de la imagen N°02. Notamos en este gráfico, una primera rama “O-A” con la misma pendiente que el sistema elástico (rama de color “azul”); pero una vez excedido el punto de cedencia, la rama “A-B” es perfectamente horizontal, con una rigidez igual a “0”. A lo largo de esta rama, es donde se desarrolla la incursión inelástica, caracterizada por presencia de deformaciones permanentes, y cuantificada en términos de ductilidad “μ” de la siguiente manera:
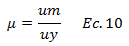
El programa NONLIN V 7.14 nos arroja la ductilidad en cada caso de estudio, y a su vez este valor será comparado con los obtenidos de la aplicación de la ecuación N°10, donde se requieren los desplazamientos máximos “um” que el programa en cuestión también arroja, siendo necesario plantear una relación, para estimar el desplazamiento cedente “uy”. Dicho planteamiento se fundamenta, en observar detalladamente el gráfico de la imagen N°02, e inferir que la rigidez lateral “K” interpretada gráficamente como la pendiente de la recta es la misma tanto para el modelo elástico como para el que incursiona en el rango inelástico una vez superado el punto cedente, por lo que se puede establecer lo siguiente:
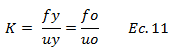
De esta ecuación, se derivan las siguientes expresiones:
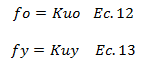
Al sustituir las ecuaciones N°12 y N°13 en la ecuación N°04 obtenemos:
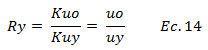
Por lo que basados en la ecuación N°14, el desplazamiento cedente “uy” es:
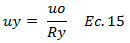.png)
Con este valor de “uy” y el desplazamiento máximo “um” que nos arroja la herramienta computacional NONLIN V 7.14, encontramos la ductilidad “μ” de una forma alternativa, y la misma será comparada con la que nos arroja el programa en cuestión. Estos valores de ductilidad obtenidos, se contrastarán con la ductilidad “μ” estandarizada en la norma sísmica COVENIN 1756-1:2001, deduciendo conclusiones de importancia, acerca de los periodos naturales de estructuras que mejor se adaptan a las ecuaciones allí establecidas. Al mismo tiempo, basados en el concepto de espectro, el cual según Chopra (2014) es:
Una gráfica del valor máximo de una cantidad de respuesta como una función del período de vibración natural “Tn” del sistema, o de un parámetro relacionado, como la frecuencia circular “ωn” o la frecuencia cíclica “fn”.
Estaremos desarrollando varios gráficos espectrales para facilitar la disertación de las ideas, graficando en el eje de las ordenadas los valores de ductilidad “μ”, relación entre desplazamientos máximos inelásticos “um” y desplazamientos máximos elásticos “uo”, y por supuesto en el eje de las abscisas los valores de periodo natural “Tn”. Procedamos a realizar las aplicaciones prácticas.
RESPUESTAS MÁXIMAS EN TÉRMINOS DE FUERZA Y DESPLAZAMIENTO PARA EL CASO ELÁSTICO
En el esquema conceptual de la imagen N°03 se ilustran la pautas para la inclusión del modelo elástico en el programa NONLIN V 7.14, resaltando los valores que nos servirán de base, en el establecimiento del punto cedente “fy-uy”, representados esencialmente por “fo-uo”. Se toma como referencia el modelo estructural con un “Tn=0.05 seg”; este procedimiento se debe realizar hasta incluir todos los valores de períodos naturales señalados en la imagen N°02, variando de forma arbitraria los valores de rigidez lateral “K”.
Imagen N°03: inclusión del modelo elástico en la herramienta computacional NONLIN V 7.14
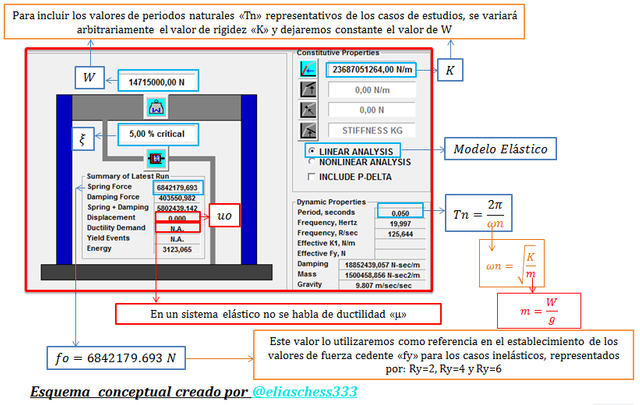
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Los gráficos resaltados en color “rojo” provienen de una captura de pantalla realizada a la herramienta computacional NONLIN V 7.14.
A continuación presento un resumen de los resultados de respuestas máximas elásticas para cada valor de “Tn”:
Tabla N°01: respuestas máximas elásticas en términos de desplazamiento máximo “uo” y fuerza máxima “Fo”
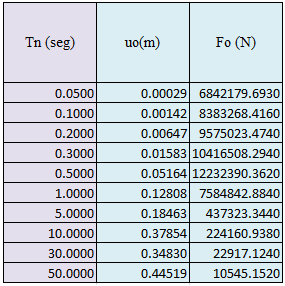
Fuente: @eliaschess333, año: 2018. Nota: tabla elaborada por el autor, la información presentada es obtenida a través de la herramienta computacional NONLIN V 7.14, y procesada con ayuda de la herramienta computacional Microsoft Excel.
Tal como se señaló en las bases conceptuales, los valores presentados en la tabla N°01, serán de utilidad en el establecimiento del punto cedente “uy-fy” para los casos de estudio inelásticos, representados por Ry=2, Ry=4 y Ry=6.
PROCESAMIENTO DE LA INFORMACIÓN ARROJADA POR EL PROGRAMA NONLIN V 7.14 PARA LOS CASOS INELÁSTICOS RY=2, RY=4 Y RY=6. CÁLCULOS TIPOS
Para este fin, es interesante mostrar cómo la condición inelástica es incluida en la herramienta computacional NONLIN V 7.14; por lo que nos valemos de los esquemas conceptuales de las imágenes N°04, N°05 y N°06, donde se aprecia la inclusión de esta condición para los distintos valores de “Ry”, y se señalan aspectos de importancia que constituyen parte de la data, que la herramienta computacional nos proporciona.
Imagen N°04: inclusión de la condición inelástica en el NONLIN V 7.14, Ry=2
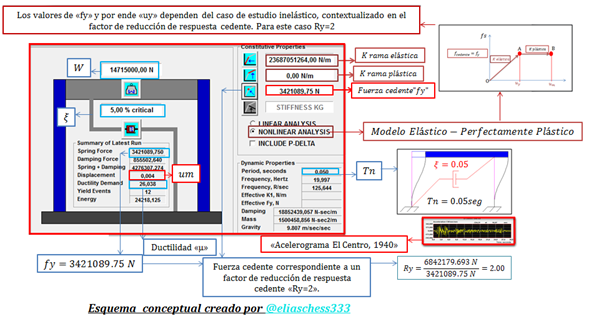
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Paint y AutoCAD V 2007. Los gráficos resaltados en color “rojo” provienen de una captura de pantalla realizada a la herramienta computacional NONLIN V 7.14.
En lo que respecta al caso inelástico representado por el factor de reducción de respuesta cedente “Ry=4” tenemos lo siguiente:
Imagen N°05: inclusión de la condición inelástica en el NONLIN V 7.14, Ry=4
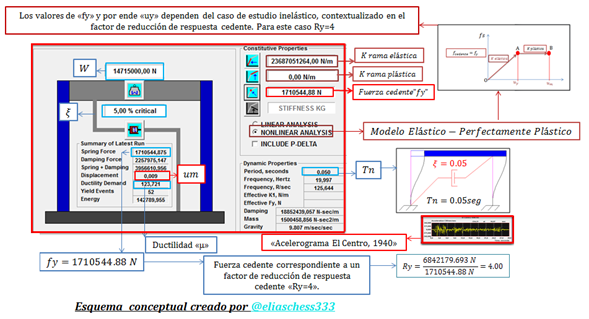
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Paint y AutoCAD V 2007. Los gráficos resaltados en color “rojo” provienen de una captura de pantalla realizada a la herramienta computacional NONLIN V 7.14.
Por su parte la inclusión del caso inelástico representado por el factor de reducción de respuesta cedente “Ry=6” viene dada por:
Imagen N°06: inclusión de la condición inelástica en el NONLIN V 7.14, Ry=6
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint, Paint y AutoCAD V 2007. Los gráficos resaltados en color “rojo” provienen de una captura de pantalla realizada a la herramienta computacional NONLIN V 7.14.
Conviene señalar que la fuerza cedente “fy” especificada en cada uno de los casos inelásticos, es obtenida con ayuda de la ecuación N°09, y a continuación se realiza un ejemplo práctico, tomando como referencia los valores de “fy” incluidos en los esquema conceptuales de la imágenes N°04, N°05 y N°06, y el modelo estructural con “Tn=0.05 seg”.
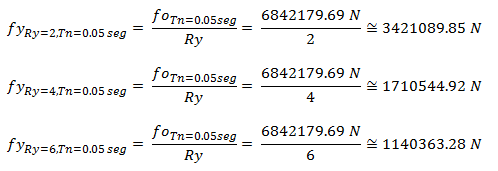
También resulta de interés práctico la determinación de los desplazamientos cedentes “uy”, y a continuación se presentan los cálculos tipos del mismo, para cada caso de estudio inelástico, y tomando como referencia el sistema estructural con un “Tn=0.05seg”.
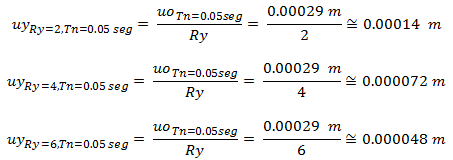
Una vez observado los cálculos tipos en pro de la determinación de “uy” y “fy” se tiene que este proceso se realiza para cada periodo natural “Tn” a estudiar, tomando en consideración los distintos casos inelásticos. En este sentido, procederemos a construir una data, como la mostrada en las tablas N°02, N°03 y N°04, donde la información de relevancia arrojada por la herramienta computacional NONLIN V 7.14 es la relativa al desplazamiento máximo “um”; vale destacar que este desplazamiento está asociado, como el máximo que la estructura ha desarrollado, posterior a la incursión en el rango de comportamiento inelástico, es decir, una vez superado el desplazamiento cedente “uy” (ver gráfico imagen N°02). Notemos que para los casos de comportamiento elástico (ver tabla N°01) al hacer mención al desplazamiento máximo, simplemente se utiliza la nomenclatura “uo” ya que no existe cedencia. En las tablas citadas se incluye una columna, contentiva del cociente que resulta de dividir el desplazamiento máximo del sistema inelástico con el desplazamiento máximo del sistema elástico “um/uo”, y que representa una forma alternativa de expresar las respuestas máximas, al momento de construir los espectros de respuestas inelásticos.
Tabla N°02: respuesta estructural sistema inelástico, Ry=2
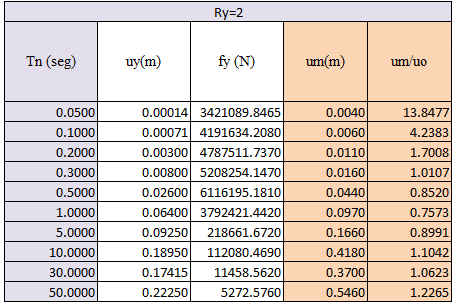
Fuente: @eliaschess333, año: 2018. Nota: tabla elaborada por el autor, la información presentada es obtenida a través de la herramienta computacional NONLIN V 7.14, y procesada con ayuda de la herramienta computacional Microsoft Excel.
Tabla N°03: respuesta estructural sistema inelástico, Ry=4
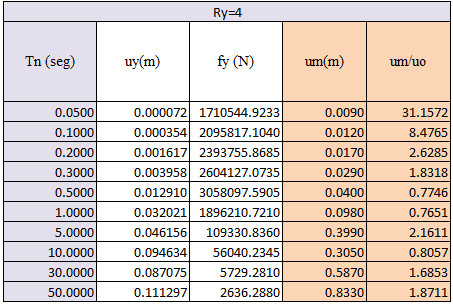
Fuente: @eliaschess333, año: 2018. Nota: tabla elaborada por el autor, la información presentada es obtenida a través de la herramienta computacional NONLIN V 7.14, y procesada con ayuda de la herramienta computacional Microsoft Excel.
Tabla N°04: respuesta estructural sistema inelástico, Ry=6
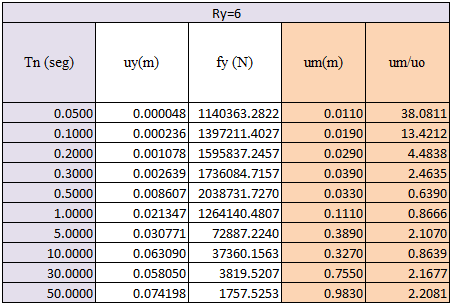
Fuente: @eliaschess333, año: 2018. Nota: tabla elaborada por el autor, la información presentada es obtenida a través de la herramienta computacional NONLIN V 7.14, y procesada con ayuda de la herramienta computacional Microsoft Excel.
Dado que se conocen los desplazamientos máximos “um” y cedentes “uy” (ver tablas N°02, N°03 y N°04), la ductilidad se puede estimar fácilmente con ayuda de la ecuación N°10, y a continuación mostramos un cálculo tipo para cada caso inelástico de estudio, tomando como referencia el sistema estructural con un “Tn=0.05 seg”.

La ductilidad se calculará para cada valor de periodo natural “Tn” y cada caso inelástico de estudio; y se contrastará directamente con el valor de ductilidad que arroja la herramienta computacional NONLIN V 7.14. En las tablas que siguen se presenta tal comparación, estimando la diferencia porcentual:
Tabla N°05: evaluación de la ductilidad “μ” para Ry=2
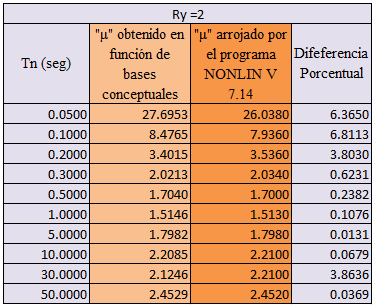
Fuente: @eliaschess333, año: 2018. Nota: tabla elaborada por el autor, la información presentada es obtenida a través de la herramienta computacional NONLIN V 7.14, y procesada con ayuda de la herramienta computacional Microsoft Excel.
Tabla N°06: evaluación de la ductilidad “μ” para Ry=4
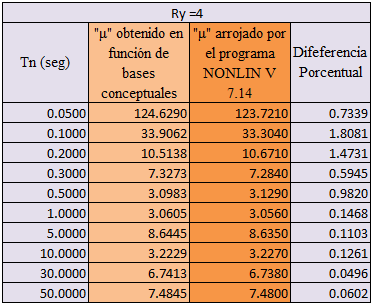
Fuente: @eliaschess333, año: 2018. Nota: tabla elaborada por el autor, la información presentada es obtenida a través de la herramienta computacional NONLIN V 7.14, y procesada con ayuda de la herramienta computacional Microsoft Excel.
Tabla N°07: evaluación de la ductilidad “μ” para Ry=6
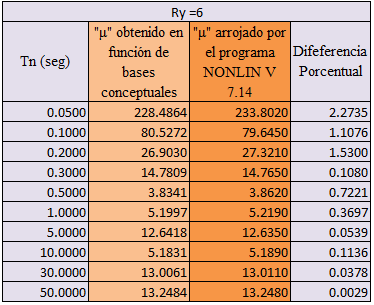
Fuente: @eliaschess333, año: 2018. Nota: tabla elaborada por el autor, la información presentada es obtenida a través de la herramienta computacional NONLIN V 7.14, y procesada con ayuda de la herramienta computacional Microsoft Excel.
De acuerdo a los resultados plasmados a lo largo de las tablas N°06 y N°07, se tiene que la diferencia porcentual entre los valores de ductilidad es menor al 5%. Por su parte en la tabla N°05, para los valores de “Tn=0.05 seg” y “Tn=0.10 seg” esta diferencia excede ligeramente el valor de 5%. Realizar estas comparaciones, y ver que los valores son cercanos, nos da confianza en el procesamiento de la información, en pro de la recopilación de la data, que nos permitirá construir los espectros de respuestas inelásticos, lo cual se realiza en el siguiente tópico.
CONSTRUCCIÓN DE ESPECTROS DE RESPUESTAS INELÁSTICOS A TRAVÉS DE UN ENFOQUE ALTERNATIVO
Recomiendo al lector, la revisión de la referencia N°05, donde se ilustra el proceso de construcción de un espectro de respuesta elástico, y así afiance conceptos de importancia en este rango de comportamiento de la estructura. Ahora bien, basados en la información presentada en el tópico anterior, procederemos a construir los espectros de respuestas inelásticos, caracterizados por el hecho, de que en el eje de las abscisas se encuentran los valores de periodo natural “Tn”, y en la ordenada las respuestas máximas, contextualizadas en este trabajo de la siguiente forma: “um/uo” y “μ”. Revisemos los gráficos de los esquemas conceptuales de las imágenes N°07 y N°08 para una mejor ilustración de las ideas:
Imagen N°07: espectros de respuestas inelásticos “Tn vs um/uo”
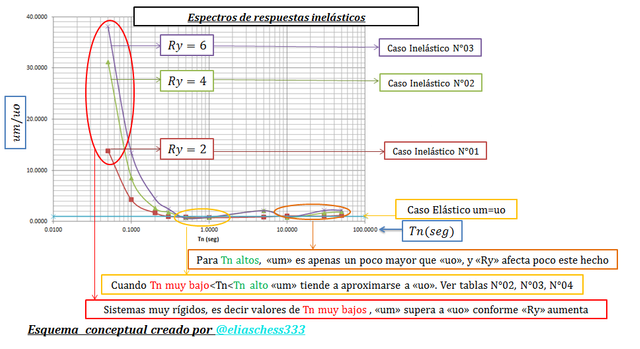
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico que se presenta fue elaborado con la herramienta computacional Microsoft Excel, con data proveniente de la herramienta computacional NONLIN V 7.14, plasmada en las tablas N°02, N°03 y N°04.
Resulta de interés plantear el espectro de respuesta inelástico de periodo natural “Tn” vs. ductilidad “μ”; tomando como referencia los valores de ductilidad arrojados por la herramienta computacional NONLIN V 7.14; apreciemos el siguiente esquema conceptual:
Imagen N°08: espectros de respuestas inelásticos “Tn vs μ”
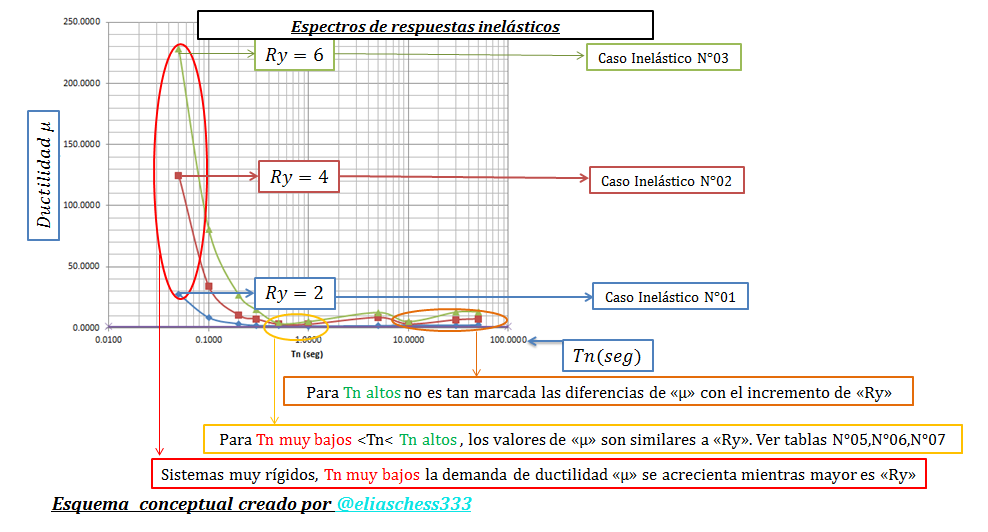
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico que se presenta fue elaborado con la herramienta computacional Microsoft Excel, con data proveniente de la herramienta computacional NONLIN V 7.14, plasmada en las tablas N°05, N°06 y N°07.
Las conclusiones principales que se desprenden del análisis de los gráficos presentados en los esquemas conceptuales de las imágenes N°07 y N°08, apuntan hacia los elevados valores de desplazamientos máximos “um” y de ductilidad “μ” que experimentan las estructuras de periodo natural “Tn” muy bajo, es decir, estructuras muy rígidas, valores que están notoriamente influenciados por el factor de reducción de respuesta cedente “Ry”. Es sorprendente, como un sistema rígido que experimenta la cedencia, exige tales demandas de ductilidad “μ”, caracterizadas por que los desplazamientos máximos “um” superan grandemente los desplazamientos máximos del sistema elástico “uo”. Surge la siguiente interrogante:
¿Y es posible en la cotidianidad un valor de ductilidad tan elevado, como ocurre por ejemplo en los sistemas muy rígidos?
Si analizamos la filosofía en que se fundamenta un sistema estructural muy rígido, es precisamente que su comportamiento tenderá a ser elástico. Ahora bien, estas condiciones de falla que se suponen en el espectro inelástico, son valores experimentales, que nos despiertan la sensibilidad a los que nos formamos en el campo de la sismoresistencia acerca de lo peligroso que puede ser la acumulación excesiva de rigidez. En las aplicaciones de la ingeniería sismoresistente, enfocadas a la evaluación de estructuras existentes, este hecho descrito en el párrafo anterior, es un concepto de importancia práctica, en lo referente a detectar concentraciones de rigidez en las estructuras que se evalúan. Un caso típico es por ejemplo, la presencia de una columna corta; en el esquema conceptual de la imagen N°09 se ilustra este hecho:
Imagen N°09: aplicación de conceptos estudiados ante la presencia de una columna corta

Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. Las imágenes corresponden al Complejo Académico Los Perozo, Coro-edo. Falcón y las mismas fueron capturadas con mi dispositivo Tablet VIT-T4000.
Se aprecia que la columna corta se produce porque gran parte de la altura de la misma está rodeada de paredes, lo que le confiere una gran rigidez, asociada a una alta demanda de ductilidad; que compromete al elemento más débil, es decir, la columna corta. Surge la siguiente cuestión:
¿Cómo se define en la norma sísmica venezolana el valor de ductilidad?
Revisemos el siguiente tópico para dar respuesta a esta interrogante.
ABORDAJE CRÍTICO REFLEXIVO DEL FACTOR DE DUCTILIDAD “μ” DESCRITO EN LA NORMA SÍSMICA VENEZOLANA COVENIN 1756-1:2001, A TRAVÉS DEL USO DE ESPECTROS DE RESPUESTAS INELÁSTICOS
La norma sísmica venezolana COVENIN 1756-1:2001 en su sección 10.1 señala para el cálculo de los desplazamientos máximos la siguiente expresión:
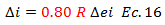
Según la norma, el significado de las variables involucradas es:
R, factor de reducción de respuesta; tratado en el desarrollo del trabajo con la forma “Ry”.
∆ei, es el desplazamiento de la estructura suponiendo que se comporta elásticamente.
Extrapolando los principios de la ecuación N°16 a las ideas disertadas en este trabajo, tenemos que “∆ei” está representado por el desplazamiento cedente “uy”, dado que hasta este punto la estructura se comporta elásticamente, y al ser superado esta comienza su incursión en el rango de comportamiento inelástico, en búsqueda de alcanzar el desplazamiento máximo “um= ∆i”, bajo un modelo de comportamiento estructural elástico-perfectamente plástico (ver gráfico imagen N°02). Basados en la ecuación N°10, tenemos que este desplazamiento viene dado por:
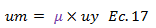
Por lo que se deduce que el término resaltado en color “rojo” de la ecuación N°16 representa aproximadamente el factor de ductilidad “μ”; siendo de interés hacer una comparación de las ductilidades obtenidas para los distintos periodos naturales “Tn” evaluados en cada caso inelástico con la herramienta computacional NONLIN V 7.14 y la ductilidad aproximada “0.8R” que establece la norma sísmica venezolana; y cómo solo depende de “R” los valores de ductilidad con los que estaremos comparando los distintos casos inelásticos vienen dados por:
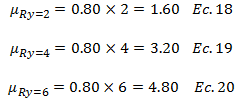
En los esquemas conceptuales de las imágenes N°10, N°11 y N°12, se realiza la comparación citada en líneas anteriores:
Imagen N°10: Comparación entre “μ NONLIN V 7.14” y “μ COVENIN 1756-1:2001”. Ry=02
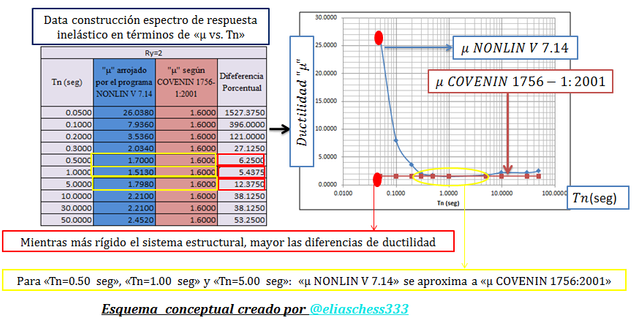
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico que se presenta fue elaborado con la herramienta computacional Microsoft Excel, con data proveniente de la herramienta computacional NONLIN V 7.14, plasmada en la tabla que se encuentra en la parte izquierda del gráfico.
Imagen N°11: Comparación entre “μ NONLIN V 7.14” y “μ COVENIN 1756-1:2001”. Ry=04
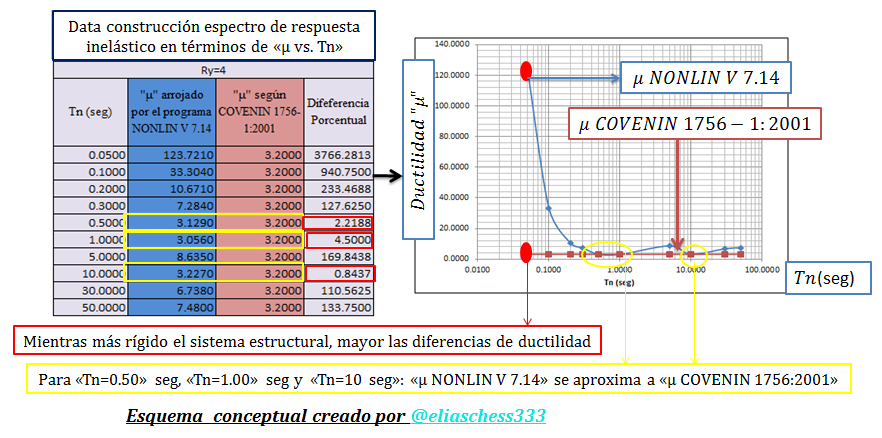
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico que se presenta fue elaborado con la herramienta computacional Microsoft Excel, con data proveniente de la herramienta computacional NONLIN V 7.14, plasmada en la tabla que se encuentra en la parte izquierda del gráfico.
Imagen N°12: Comparación entre “μ NONLIN V 7.14” y “μ COVENIN 1756-1:2001”. Ry=06
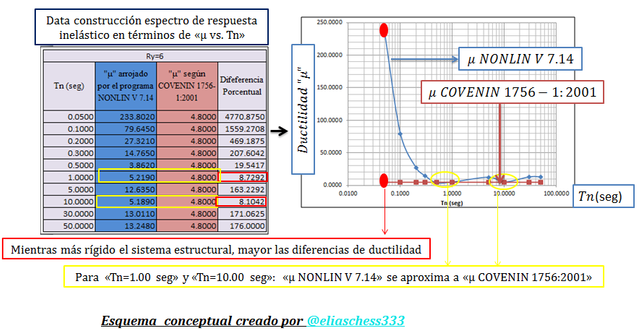
Fuente: @eliaschess333, año: 2018. Nota: esquema conceptual elaborado por el autor, con ayuda de las herramientas Microsoft PowerPoint y Paint. El gráfico que se presenta fue elaborado con la herramienta computacional Microsoft Excel, con data proveniente de la herramienta computacional NONLIN V 7.14, plasmada en la tabla que se encuentra en la parte izquierda del gráfico.
Del estudio de los esquemas conceptuales presentados a lo largo de las imágenes N°10, N°11 y N°12, se desprende que el factor de ductilidad que establece la norma sísmica venezolana se ajusta a los valores ductilidad obtenidos con el uso de la herramienta computacional NONLIN V 7.14 para ciertos valores de períodos naturales “Tn”.
Desde mi percepción, considero que la norma sísmica Venezolana 1756-1:2001 basada en el factor de reducción de respuesta “R”, fija una demanda de ductilidad tope en las estructuras, que se ajusta muy bien a estructuras que no caen en la zona de máxima rigidez (“Tn” muy bajo) ni máxima flexibilidad (“Tn” muy alto). Lo cual tiene mucho sentido, dado que la norma en cuestión se enfoca a edificaciones sismoresistentes, es decir, que valores de períodos naturales muy altos no son típicos en las edificaciones Venezolanas y valores de periodos muy bajos (estructuras muy rígidas) generarían excesivos costos al momento de construirse; de manera tal que la ductilidad normativa aplica con bastante precisión a las edificaciones venezolanas.
Lo anterior expuesto se complementa con las fórmulas alternativas para el cálculo de periodo natural que establece la norma; por ejemplo en la sección 9.3.2.2, para edificaciones aporticadas se señala la siguiente fórmula:
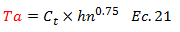
Donde “hn” es la altura de la edificación medida desde el último nivel, hasta el primer nivel. El término “Ct” es igual a “0.07” para edificaciones de concreto armado. Realicemos unos cálculos tipos para distintos valores de “hn”, sustituyendo este valor en metros “m”:
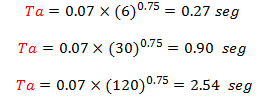
Estos resultados complementan la idea de que las edificaciones venezolanas, se encuentran en esa zona intermedia, delimitada por la máxima rigidez y la máxima flexibilidad.
CONCLUSIONES
En la formación como ingenieros sismoresistentes, es importante resaltar, que debemos concebir a nuestras edificaciones, como sistemas estructurales que ante la ocurrencia de sismos, pueden ceder, y es nuestro reto, garantizar una adecuada incursión en el rango de comportamiento inelástico de la estructura en cuestión; lo que redunda en una excelente labor de cálculo. Ahora bien, los criterios básicos que giran en torno al análisis inelástico de las estructuras, se explican con bastante satisfacción con el uso de espectros de respuestas inelásticos, a continuación a modo de conclusiones se hace un resumen de tales criterios:
Sistemas extremadamente rígidos, caracterizados por períodos naturales “Tn” muy bajos, desarrollan valores sorprendentes de demanda de ductilidad, cuando se supone una cedencia en los mismos, al ser sometidos a una excitación sísmica.
Lo anterior permite despertar cierta sensibilidad, hacia lo vulnerable que puede ser una edificación, ante grandes concentraciones de rigidez, dado que como la estructura es un todo, esta demanda será a modo metafórico delegada a los elementos más débiles; un ejemplo típico de este hecho, es la presencia de columnas cortas. Te invito a la revisión de la referencia N°06 donde hago un abordaje de este tema.
Al fijar el factor de reducción de respuesta “R” conforme a la norma sísmica venezolana COVENIN 1756-1-2001, debemos ser conscientes que mientras más alto sea, mayor es el nivel de ductilidad a desarrollar por la estructura.
El comportamiento dúctil de las estructuras ante la ocurrencia de sismos, está condicionado a la aplicación de criterios sismoresistentes en su proceso de análisis, diseño y construcción. En próximas publicaciones estaré abordando los criterios sismoresistentes para el diseño estructural en concreto armado.
Finalmente es interesante resaltar, que las ideas inferidas del análisis de cada uno de los gráficos presentados, nos permiten tener una mejor comprensión conceptual de la ecuación diferencial de equilibrio dinámico del sistema estructural (Ecuación N°08), te invito a que la repases y amplíes los conocimientos, con tus propias conclusiones.
Espero este post haya sido de su agrado. Es todo un placer escribir contenidos para nuestra sub-comunidad científica de #stem-espanol y comunidad científica #steemstem. Nos leemos en otra oportunidad.
FUENTES DE INFORMACIÓN CONSULTADAS
1.- CHOPRA ANIL K. 2014. DINÁMICA DE ESTRUCTURAS. CUARTA EDICIÓN. PEARSON EDUCACIÓN, MÉXICO.
2.- NORMA VENEZOLANA. EDIFICACIONES SISMORESISTENTES. PARTE 1: REQUISITOS. 1ERA REVISIÓN. COVENIN 1756-1:2001
3.- NONLIN “EDUCATIONAL PROGRAM FOR LEARNING THE CONCEPTS OF STRUCTURAL DYNAMICS AND EARTHQUAKE ENGINEERING”. DEVELOPED BY DR. FINLEY CHARNEY, NONLIN IS AVAILABLE AS ONLINE TOOL THROUGH NEESHUB: HTTP://NEES.ORG/
LECTURAS RECOMENDADAS
4.-SANTANA E. 2018. APLICACIONES DE LA DINÁMICA ESTRUCTURAL EN EL ESTUDIO DE LA RESPUESTA INELÁSTICA EN EL TIEMPO DE UN SISTEMA DE UN GRADO DE LIBERTAD SOMETIDO A UNA EXCITACIÓN SÍSMICA EN LA BASE. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/aplicaciones-de-la-dinamica-estructural-en-el-estudio-de-la-respuesta-inelastica-en-el-tiempo-de-un-sistema-de-un-grado-de
5.- SANTANA E. 2018. APRENDIENDO A CONSTRUIR UN ESPECTRO DE RESPUESTA ELÁSTICO A PARTIR DE LA EXCITACIÓN SÍSMICA DE SISTEMAS DE UN GRADO DE LIBERTAD. APLICACIONES EN LA INGENIERÍA SISMORESISTENTE. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/aprendiendo-a-construir-un-espectro-de-respuesta-elastico-a-partir-de-la-excitacion-sismica-de-sistemas-de-un-grado-de-libertad
6.- SANTANA E. ESTUDIO DEL EFECTO DE COLUMNA CORTA EN EDIFICACIONES DE CONCRETO ARMADO, DESDE EL ENFOQUE DE LA INGENIERÍA SISMORESISTENTE. DISPONIBLE EN: https://steemit.com/stem-espanol/@eliaschess333/estudio-del-efecto-de-columna-corta-en-edificaciones-de-concreto-armado-desde-el-enfoque-de-la-ingenieria-sismoresistente-con-el
Muy buenos esquemas conceptuales y como siempre buen artículo, excelente organización del contenido.
Gracias estimado @ydavgonzalez. Veo en los esquemas conceptuales una excelente herramienta para hacer más didáctica la disertación de las ideas. Saludos!!!
siempre tu post son verdaderamente interesante amigo, felicidades siempre pendiente de tus publicaciones
Complacido de que estés al tanto de mis publicaciones, agradecido por el apoyo. Saludos estimado @gerardoalfred!
Gracias por educarnos en esta área @eliaschess333. Saludos.
Lo hago con mucho cariño y esfuerzo, gracias por el apoyo estimada @elvigia. Saludos!
Realmente este es un muy buen artículo. Excelente redacción y detalles muy bien desarrollados. Te felicito por el apoyo alcanzado. Mis cordiales saludos.
Gracias estimado @tsoldovieri, muy motivador tu comentario, me alegra que te haya gustado este artículo. Saludos!
Impresionante, saludos