Arithmetic Series
Hello there. This math post is on finding the total of all numbers in an arithmetic sequence. The sum/total of an arithmetic sequence is called an arithmetic series.
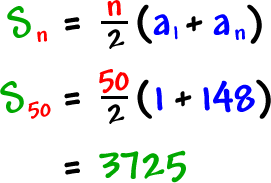
Sections
- A Review Of Arithmetic Sequences
- Arithmetic Series Definition & Formula
- Worked Examples
A Review Of Arithmetic Sequences
Arithmetic sequences is a list of ordered and patterned numbers. The pattern is set up in such a way such that the next number increases/decreases by the same amount.
Examples of arithmetic sequences include:
A Formula For Finding Numbers In An Arithmetic Sequence
Let the first term in an arithmetic sequence be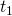 
and let 
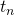be the n-th number in an arithmetic sequence. The common difference between any two consecutive numbers in an arithmetic sequence be denoted by d.
The formula for the n-th number in an arithmetic sequence is:
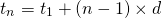
In the arithmetic sequence 25, 29, 33, 37, 41, 45, 49, 53, ... , the common difference is 4, the first term is 25. The sixteenth term in the sequence can be determined with the above formula. (I use the letter t, other people may use the letter a.)
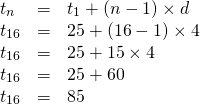
Arithmetic Series Definition & Formula
What if you wanted the total or sum of all the numbers in an arithmetic sequence (that is finite)? This is where arithmetic series and its formula comes in.
The arithmetic sequence of 1, 2, 3, 4, 5, 6, 7, 8, ..., 32 has an arithmetic series of:
The total of the whole numbers (natural numbers) from 1 to 32 is 528. This total can be evaluated with algebra steps of:
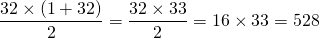
General Formula
- Denote
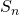as the sum or total of the first nnumbers in an arithmetic sequence. 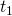- : The first term in an arithmetic sequence
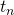: the n-th number in an arithmetic sequence.- n : the number of terms in the arithmetic series.
The sum/total of n numbers in an arithmetic sequence is given by the formula:
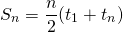
An alternate version of this sum formula is using the definition of 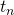along with algebra and simplifying.
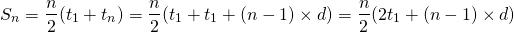
Worked Examples
Example One
What is the total of the positive whole numbers from 1 to 20?
The arithmetic series here looks like:
The first term is 1, the last term is 20 and there are 20 numbers in this series. With the arithmetic series formula, the calculations look something like this:
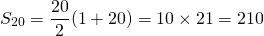
Example Two
What is the total of the arithmetic series -11 - 15 - 19 - 23 - ... - 67?
In the first example, it was (somewhat) obvious that the number of terms is 20. In this second example, it is not as simple. The number of terms in the series needs to be determined before using the arithmetic series formula.
The first term is -11, the last term is -67 with a common difference of -4.
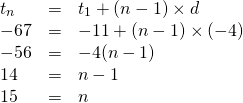
With n = 15, the series formula can be used.
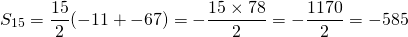
The sum -11 - 15 - 19 - 23 - ... - 67 is equal to -585.
Example Three
A young boy named Robert receives an allowance each week for twelve weeks. The first week's allowance is $5, the second week's allowance is $10, and each week's allowance increases by $5 per week.
- What is the final allowance amount?
- How much allowance money does Robert accumulate over the twelve weeks?
For the first question, the sequence looks something like 5, 10, 15, 20, ..., Twelfth allowance.
The first allowance is 5, the common difference is 5 and the number of weeks is 12. The twelfth allowance can be determined with the arithmetic sequence formula.
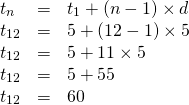
The final allowance amount is 60 dollars.
To find out how much Robert has earned over the twelve weeks we add the allowance money together from each week. That is we find the total/sum of 5 + 10 + 15 + 20 + ... + 60.
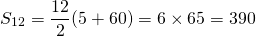
Over the 12 weeks, Robert has received $390 in allowance money.
- Math text and images done in LaTeX with QuickLaTeX.com
- Reference book: Functions 11 by Nelson-Thomson (2008)
Geometry and math very interesting. https://steemit.com/@merveakbulut
Look at my posts, Please. I am a student. I will teacher😊
o my God... you posts in math are superb... I love math ...but not good in posting.....