PROOF: The reflective property of a parabola

For this proof, the parabola y^2=4ax will be used, where point P = P(at^2, 2at)
To prove the reflective property of the parabola, it must be proven that RF= FP as this would form an isosceles triangle, meaning angles PRF and RPF are equal. Consequently, angle RPF must be equal to the angle between the reflected beam and the tangent at P as they are vertically opposite angles. The angle between the reflected beam and the tangent at P is equal to the angle of the line through P parallel to the x axis because the angle of the line through P and angle PRF are alternate angles, and it is known that angle PRF is equal to angle RPF, which is also equal to the angle between the reflected beam and the tangent at P. Hence, reflected rays will appear to emanate from the focus because FP directly corresponds to the outwards appearance of the beam due to the equality of the angles. If point P were to shift along the parabola, the line FP would also move, altering the angle RPF and consequently the angle between the reflected beam and the tangent at P.

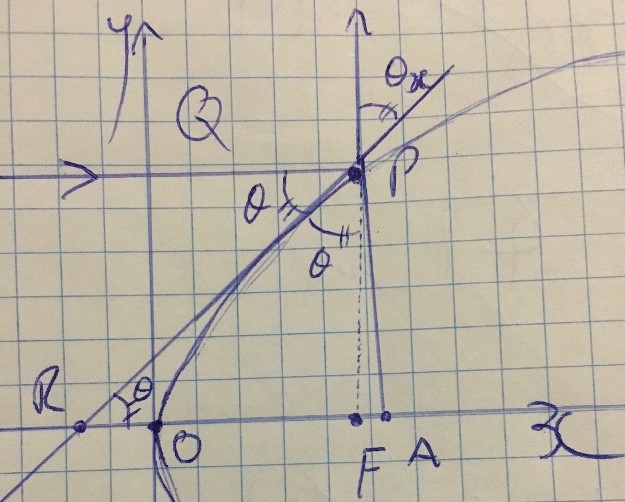
PA is the distance perpendicular to the x axis, the y value of P, = 2at
OA is the x value of P= at^2
OF = a, therefore FA = (at^2-a)
FP= FP (unknown)
Angle PAF = 90 degrees, FP = hypotenuse
c^2 = a^2+b^2
a = PA = 2at , b = FA = (at^2-a)
c^2 = (2at)^2+(at^2-a)^2
c^2 = 4a^2t^2 + a^2t^4 - a^2t^2 - a^2t^2 + a^2
c^2 = 2a^2t^2 + a^2t^4 + a^2
c^2= a^2(t^4+t^2+t^2+1)
c^2= a^2(t^2+1)^2
c= √ a^2(t^2+1)^2
c= a(t^2+1)
c= at^2+a , FP = (at^2+a)

Prove that FP= RF
RF= gradient of tangent at point P

m= (y2-y1)/ (x2-x1)
m= the derivative of the equation of the parabola which equals the slope of the line (change in y over change in x), hence m=y’

Using implicit differentiation;
y^2= 4ax
y’= d(y^2)/d(y)
d(y^2)= 4a
d(y)= 2y
y’= 4a/2y
y’= 2a/y

RF= x1 + a

(2a/y)= (y2-y1)/ (x2-x1)
y2= 2at , y1= 0 , x2= at^2 , x1= x1
(2at-0)= (2a/y)(at^2-x1)
y= (2a/y)(at^2-x1)
y.y= 2a(at^2-x1)
y^2= 2a(at^2-x1)
4a^2t^2= 2a(at^2-x1)
(4a^2t^2/2a) = (2a(at^2-x1))/2a
2at^2= at^2-x1
x1= at^2-2at^2
x1= -at^2
RF (magnitude) = (at^2+a)
RF= FP
(at^2+a)= (at^2+a)

Therefore RF= FP and the triangle RPF must be isosceles. This indicates that angles PRF and RPF are equal, as an isosceles triangle has two equal sides and two equal angles.
Light appears to emanate from the focal radius because angle RPF and theta x are vertically opposite and equal as a result. Angle Q and PRF are also equal as they are alternate angles. Angle PRF is known to be equal to angle RPF which is equal to theta x, hence angle Q is equal to theta x and angle RPF as a result. This means that the angle of the incident beams at Q will be equal to the angle of the reflected beams at theta x. Although the beam will appear to emanate from the focus because angle RPF also directly corresponds to these angles and as FP moves, the angle RPF will change, resulting in an equal change of angles Q and theta x. Essentially, the reflected beam could also be seen as an extension of FP outside of the parabola.